计组P0课下作业总结

P0.Q1 CRC校验

使用Logisim搭建一个除数为四位，原数据帧为8位的CRC校验码计算电路，模块端口定义如下：

信号名 方向 描述
A[7:0] I 8位原数据帧
B[3:0] I 4位除数
C[10:0] O 8位原数据帧+3位校验码

校验方法：将原帧补上( 除数位数 -1 )个 0 作为被除数，然后进行模二除法即可。举个例子，我们要发送的帧A为 10011，发送端和接收端共同选定的除数B为 1110。因为 B 是 4 位二进制数，我们需要在 A 的后面补上 3 个 0，从而得到 A’=10011000。我们将 A’ 作被除数，B 作除数，进行”模二除法”。如下图：

最后得到的余数是一个三位数(注意如果不是三位，也要在前面补零来凑齐三位)，这就是要求的校验码。我们将得到的校验码 110 拼接在原数据帧的后面，就得到了要发送的新帧 A’’=10011110。这样就完成了 CRC 校验码的生成。

层次化目标：

  • 设计四位模二除法器
  • 使用四位模二除法器搭建 8 位 CRC 校验码计算电路

（模二除法：它与算术除法类似，但在做减法时既不向上借位，也不比较除数和被除数相同位数值的大小；它的运算法则为1-1=0，0-1=1，1-0=1，0-0=0，例如1100-1001=0101）

四位模二除法器的构建：

信号名 方向 描述
A[3:0] I 4位被除数
B[3:0] I 4位除数
C[2:0] O 3位余数
D O 1位商
  • 思路：所谓四位模二除法器只有两种情况：当被除数最高位为1时，商恒为1，余数即为被除数和除数的按位异或结果，当被除数最高位为0时，商恒为0，余数即为被除数第三位，因此可以分别输出这两种方法算出的商（利用最高位是否为1进行分辨），放入MUX选择，利用商为0为1进行选择输出。

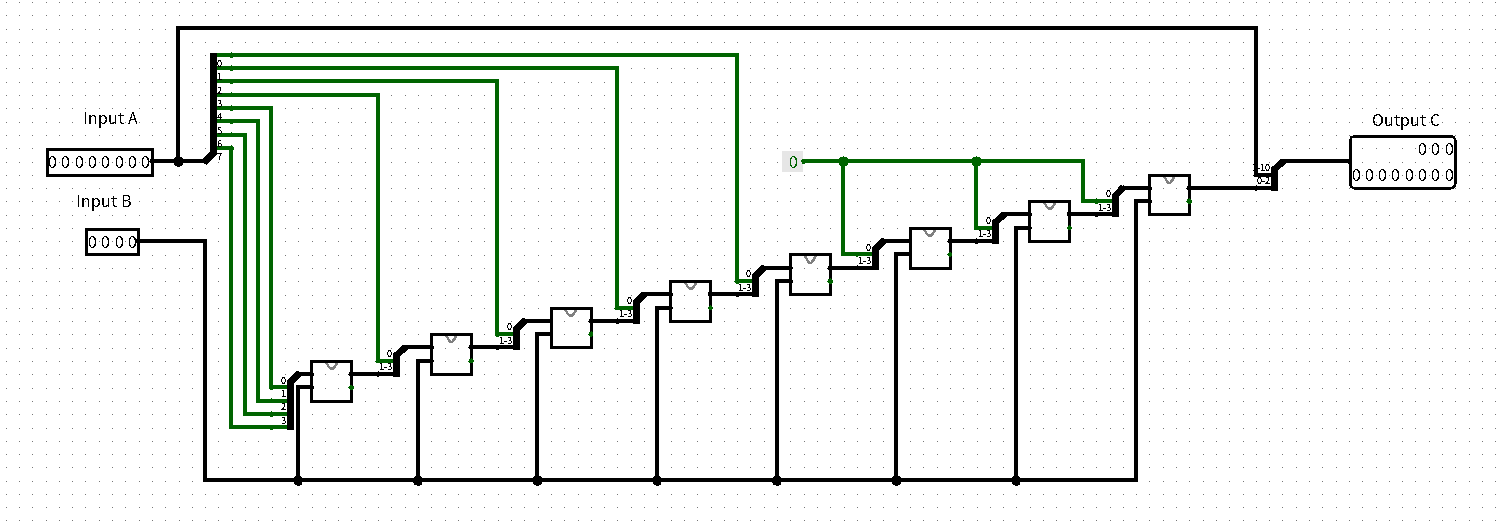
CRC校验电路的组成：

  • 思路：对于输入的被除数，从最高位四位和除数进行除法器运算，取出余数再和低一位的数组成新被除数，继续取余，直到最后被除数全部输入，这是还要连续往被除数中加3个0进行取余，最后取出的余数连接到被除数后（Spliter）输出即可。

P0.Q2 实现GRF

使用logisim搭建一个GRF

  • GRF中包含32个32位寄存器，分别对应0~31号寄存器，其中0号寄存器读取的结果恒为0。具体模块端口定义如下：

    信号名 方向 描述
    clk I 时钟信号
    reset I 复位信号，将32个寄存器中的值全部清零，1：清零、0：无效
    WE I 写使能信号，1：可以向GRF写入数据、0：不能写入数据
    A1 I 5位地址输入信号，指定32个寄存器中的一个，将其中存储数据读出到RD1
    A2 I 5位地址输入信号，指定32个寄存器中的一个，将其中存储数据读出到RD2
    A3 I 5位地址输入信号，指定32个寄存器中的一个作为写入的目标寄存器
    WD I 32位数据输入信号
    RD1 O 输出A1指定的寄存器中的32位数据
    RD2 O 输出A2指定的寄存器中的32位数据

  • 模块功能定义如下：

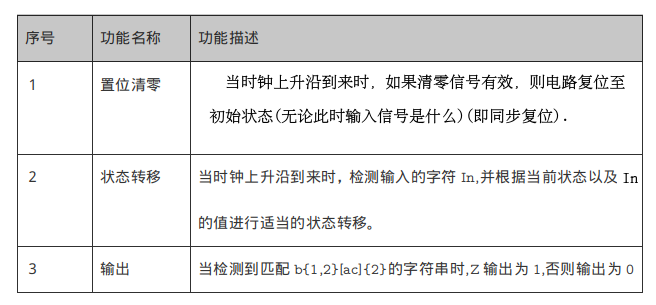
    序号 功能名称 描述
    1 复位 reset信号有效时所有寄存器存储数值清零，行为和logisim自带register的reset接口完全相同
    2 读数据 读出A1,A2地址对应寄存器中存储的数据到RD1，RD2
    3 写数据 当WE有效且时钟上升沿来临时，将WD写入A3所对应的寄存器中

  • 要求0号寄存器读出的数据在任意时刻都为0

  • 思路：

  • 1.首先考虑输入，即A3和WD（还要考虑WE的影响），考虑到A3对输入地址有选择的效果，可以考虑使用多路选择器MUX，将A3输入作为选择输入。同时利用缓冲器，当WE的输入为0时就利用缓冲器阻拦WD的输入，达到使能的效果。注意，本题中MUX需要打开三态开关，这样可以在一条通路没有被选择时断开而不是置零，如果不打开的话每个时钟上升沿都只有被选择的寄存器置数，其他都被置零。

  • 2.考虑寄存和CLK，Reset。很明显本题的储存是利用32个32位寄存器完成，而每个寄存器都需要接入clk和reset信号以达到效果，同时每一个寄存器都需要一个输入和一个输出信号，为了美观可以都使用tunnel进行构建。（由于0号寄存器只能输出0，因此可以不设置输入）

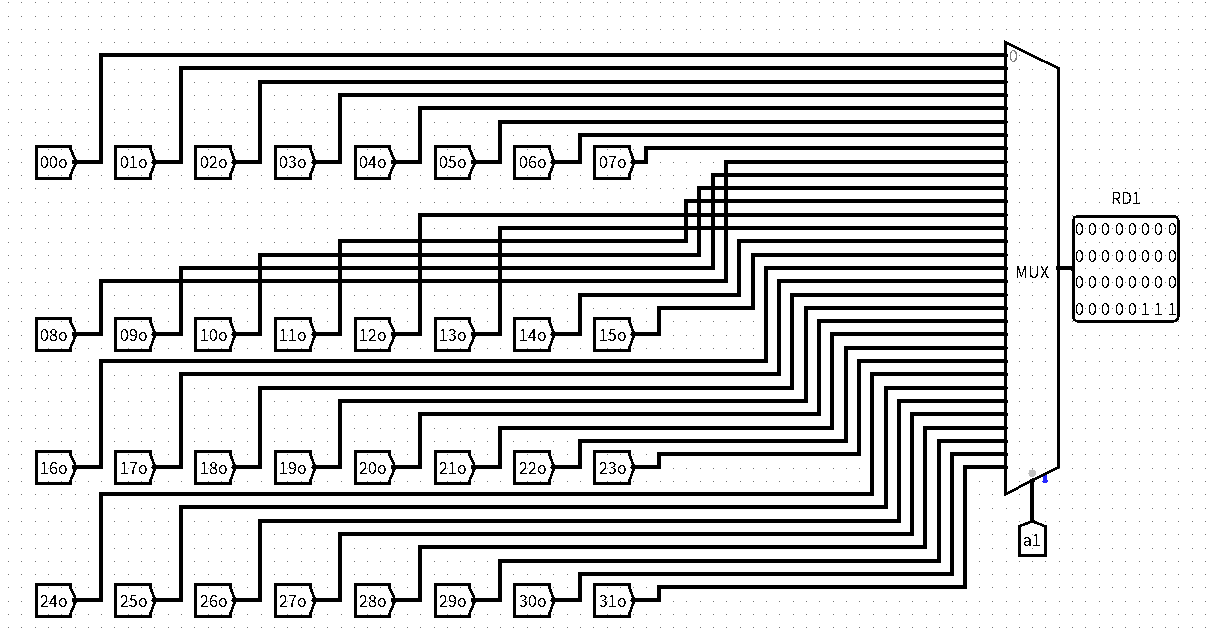
  • 3.输出就是输入的反过程，利用解复用器DMX就可以进行输出的选择，因此只需要利用五位的A1和A2进行选择输出即可。下图为A1，A2完全相同。

  • 反思：本题我的做法过于简单粗暴，因此导致布线过于凌乱，应该采取模块化思路进行分块完成，比如我之前思路提到的三部分就可以分开完成，这样的解答较为优雅。

P0.Q3 Logisim导航

  • 计小组只能往东南西北四个方向行走，且若能行走，则每次只能行走一格。若下一步不存在机房让计小组行走，那么计小组会撞到墙壁并且hit置高一周期，此时计小组仍保持原地不会移动，等待下一周期再进行运动。（如果下一步依旧撞墙， 则hit仍然置高；若下一步不会撞墙，则计小组将会继续行进，hit在此周期置0）

  • 计小组走到B机房后，“到达”信号需要置位，并保持一周期。到达B机房后计小组将会在下一周期回到原点，（下一周期的输入将被忽略掉）等待下下周期的输入，继续测试他的序列。

  • 要求使用Moore型有限状态机

  • 端口定义：

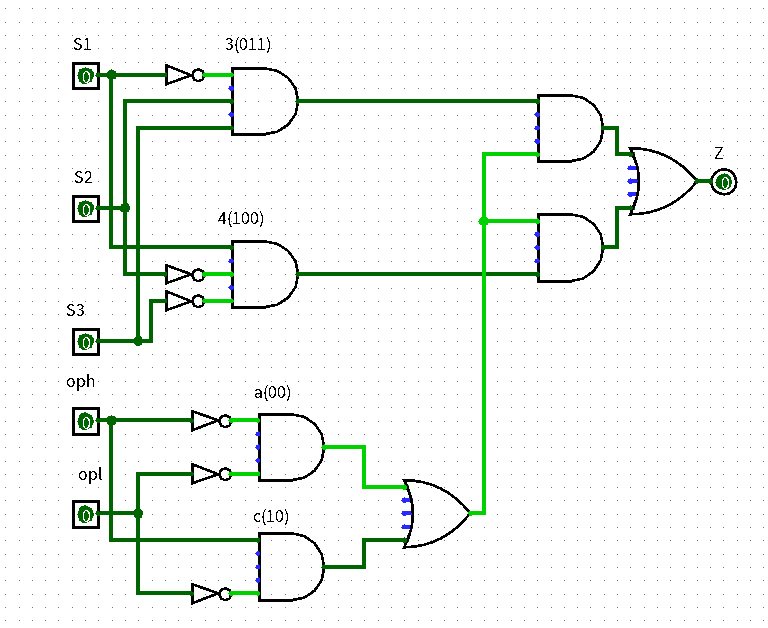
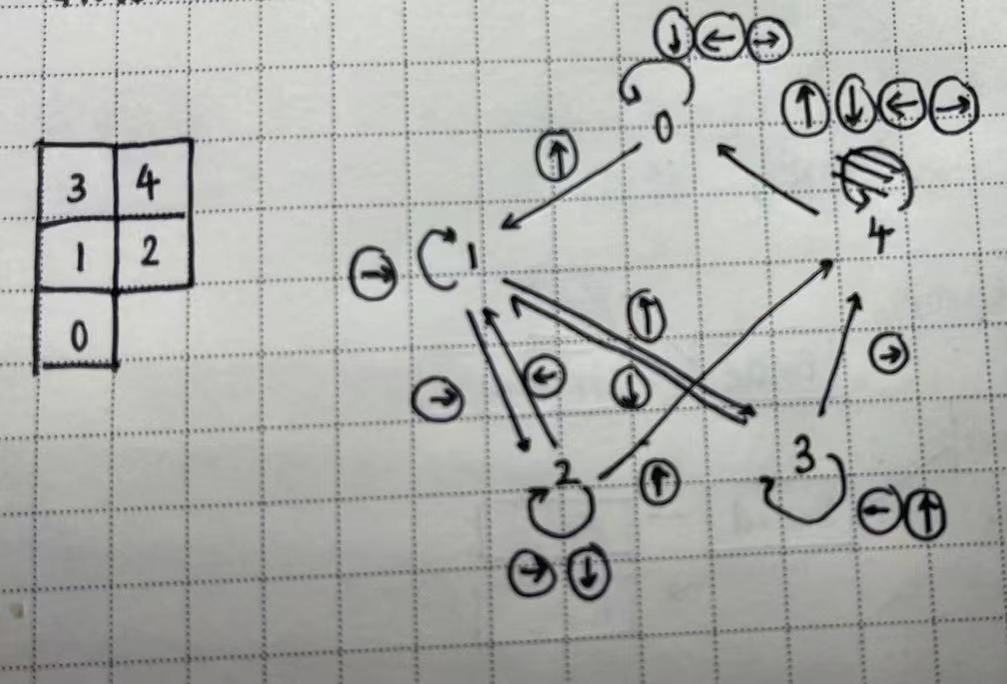
    信号名 方向 描述
    dir[1:0] I 表示行走的方向：00：向北走 01：向东走 10：向南走 11：向西走
    clk I 时钟信号
    reset I 异步复位信号
    arrive O 是否到达
    hit O 是否撞上墙壁

  • 1.构建次态逻辑（状态图，真值表）

    然后将真值表利用Logisim进行分析就能给出次态逻辑电路。（由于本题需要五个状态，四种操作，所以需要三位状态输入和两位操作输入，另外Hit输出也能够通过输入和操作判断，在这里也可以一并计算）（大概输入输出如下，截取不全）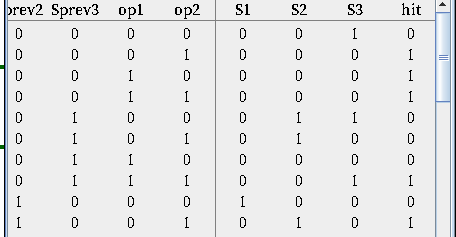

    这样次态逻辑电路就构建完成了。

  • 2.构建储存电路
    正常的三维数据输入输出，加上时钟输入端clk和复位输入端reset即可。

  • 3.构建输出电路
    由于是Moore型状态机，因此输出只和状态有关，利用比较器判断出状态编码分别是”1“”0“”0“（状态4）即可输出到达，否则未到达。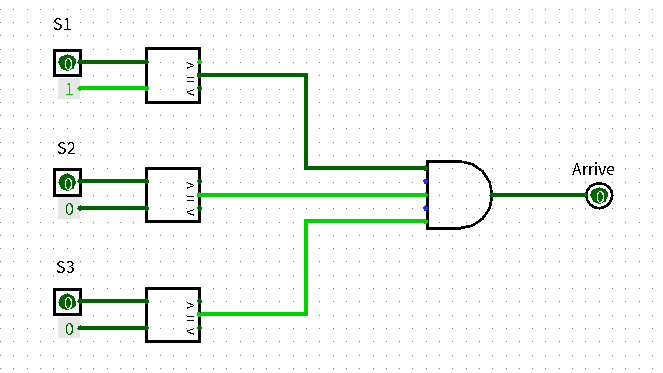

  • 4.组成整个电路
    按照正常的状态机的组成即可组装，具体略。要注意hit信号的输出也是每个周期才有所改变，因此在次态逻辑中的Hit输出值同样要用寄存器进行储存。

P0.Q4 Logisim中的FSM

  • 使用Logisim搭建一个Mealy型有限状态机，检测串行输入字符串中的能匹配正则表达式b{1,2}[ac]{2}的子串并输出。具体模块端口定义如下：

  • 模块功能定义如下：

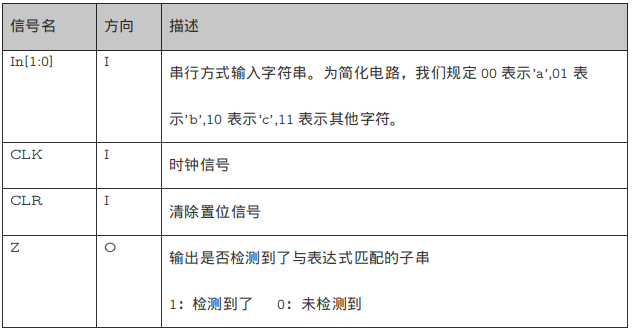
  • 注意: 每当匹配到一个子串时，需要输出一次1。例如对字符串bacbacac,模块应当在第1个c输入和第2个c输入时输出1,而在其他时刻保持输出为0

  • 注意：有限状态机的设计是Mealy型有限状态机

  • 1.构建次态逻辑电路（状态图+真值表）

    (一共6个状态，logisim自动生成即可)

  • 2.构建储存电路
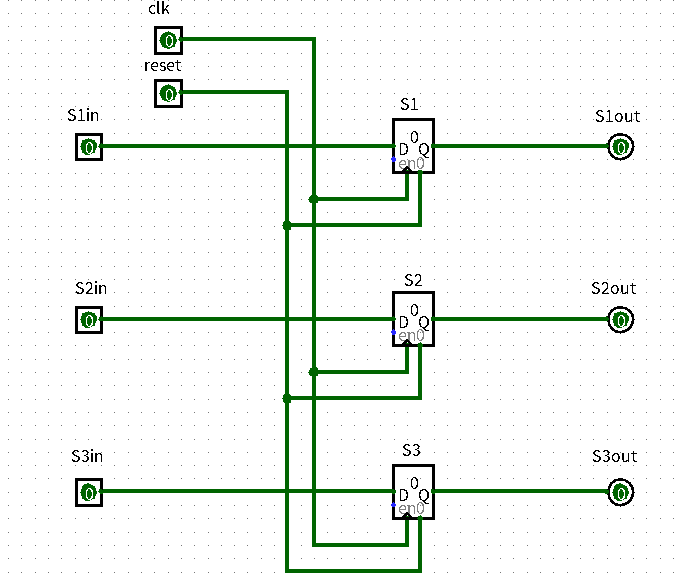
    经典的五输入（S1,S2,S3,CLK,Reset）三输出（S1,S2,S3）结构，唯一的问题在于要求同步复位，这代表只有在上升沿复位信号会发动，清空寄存器。一开始我的电路存在bug，如下图。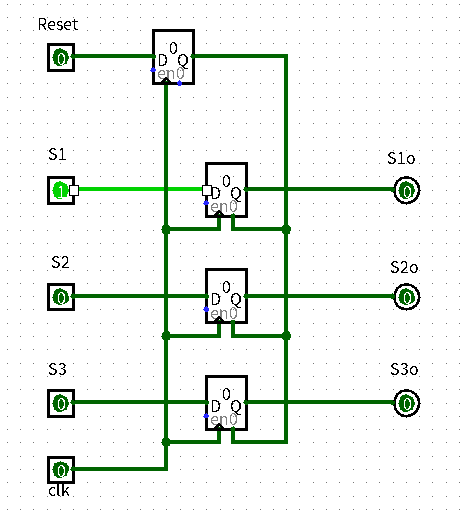

    这种电路的思路是利用寄存器寄存reset信号，直到上升沿才能输出。但是问题在于，在下一个上升沿之前这个reset信号一直有效，而经过测试，在下一个上升沿时优先判定寄存器左端输入，这个瞬间reset信号还没有归0，因此导致新的状态无法读入，因此出现Bug，所以我用了另一种方法来完成同步复位（感谢华哥）

就是利用reset信号取反后和状态分别与门连接。这样如果reset信号为1，自然与门输出0，在下一个上升沿时就可以把0写入寄存器，即清空。而reset信号为0时，输出取决于状态的输入，因此不影响正常的工作。

  • 3.构建输出电路
    此处的输出电路需要同时对读取的状态以及当前的操作进行处理（因为要求meely型状态机，需要利用当前操作进行“预判”）其实也可以让Logisim自动生成逻辑，但是我自己写了一个，相当于只有在“b[a/c]”或“bb[a/c]”条件并下一个操作为a/c时可以输出1。如下图。

  • 4.总结
    将这三个模块进行meely型连接即可（即输入也要连到输出电路模块处），但是进行Logisim测试时要注意，测试时电路会在之前输入为“ba”时就直接输出1，究其原因，是人无法同时点击clk和操作输入。因此你在点击clk时没改变a，相当于又多输入了一个a，判定到ba和输入a自然输出1。如果想测试，可以在输出1时将输入改成b”01”，此时如无意外输出会立刻变成0。
    下图为合成的fsm电路。（接线接的有点丑陋）

P0附加题：ftoi

使用Logisim进行组合逻辑设计，要求输入一个16位的单精度浮点数（符合IEEE-754标准），输出该浮点数的整数部分(包含符号)，用32位二进制符号数表示。
具体如图，有四种情况：


以及两个例子：

  • 其实可以将其和十进制的科学计数法进行对比，最高位是符号位，中间五位和01111相减后是指数位，决定小数点左右移动程度，然后最后是数字位，相当于1.023 * 10^3中的“.23”，如果中间五位不是00000则需要记得小数点前还有一个没被显示的“1”，而若为00000则只有小数部分不需要补充前导1。具体端口定义如下：

    信号名 方向 描述
    float[15:0] I 16位半精度浮点数（IEEE-754标准）
    int[31:0] O 该浮点数的整数部分（带符号），用32位符号数的补码来表示，超出表示范围则取低32位。 第3类Infinity和第4类NaN为了简化直接输出0即可

  • 思路：
    其实就是移位思路，相当于如果指数是正数，则整数部分就是小数部分的前几位，而如果指数是负数，整数部分恒为0。
    具体到这个题上，后两种情况（指数为全1）输出0，第二种情况（指数全为0）其实也只能输出0，因为此时本来整数位就为0，而00000-01111也肯定为负，此时整数位必然为0。因此只考虑指数为00000与11111之间情况。
    对于这种情况，其实也可以分成两种。当指数-01111为负数时，相当于小数点左移，但小数点前只有一位1，则此时输出也一定为0。只需要考虑指数为0或正数。
    下面给出电路图：

通过下面这个or gate可以发现把之前提到的三种输出必为0的情况进行汇总，在多路选择器中确保当其中一种情况发生时直接选择输出常数0。

而对于正常需要计算的情况，先分离中间5位和01111做减法，求出左移位数并进行左移，然后此时取高位（相当于整数部分）作为输出的低位，并在高位补0形成一个新的32位二进制数。

这里的关键在于：如何判断符号位并求补码？首先我们需要知道logisim中的补码器就是单纯的取反加1。我的思路是：首先将其的符号进行判断，利用输入的最高位，如果是0，则直接原样输出，因为正数的补码就是其本身。如果是1呢？此时要注意我们形成新32位时一定最高位不能补符号位，而是应该补0。假设是负数，那么最高位补0相当于其相反数。而相反数是正数，其补码是自身，而要求原先负数的补码，就只需要对对应正数的补码取反加一即可。此时即可应用Logisim中的补码器了。最后进行选择输出即可。

终于把P0课下作业做完了~希望第一次上机一定要过啊QAQ