计组P2课下作业总结

P2.Q1 矩阵乘法

• 题面
  使用MIPS汇编语言编写一个具有矩阵相乘功能的汇编程序。

1. 首先读取方形矩阵的阶数n，然后再依次读取第一个矩阵（n行n列）和第二个矩阵（n行n列）中的元素。
2. 两个矩阵的阶数相同，我们提供的测试数据中0<n≤8,每个矩阵元素是小于10的整数。
3. 最终将计算出的结果输出，每行n个数据，每个数据间用空格分开。评测机会自动过滤掉行尾空格以及最后的回车。
4. 请使用syscall结束程序：

   li $v0,10
   syscall

5. 不考虑延迟槽。

• 样例
  

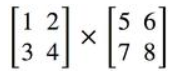
输入：
2 1 2 3 4 5 6 7 8（此处空格输入时都为回车)
输出：
19 22
43 50

• 思路
  其实我对MIPS编写现在的思路就是先用C语言想一遍应该怎么编写，然后再利用汇编语言进行翻译。我将这道题拆分成几个部分：

1. 数据空间的申请和数据初始化
   在C语言中，要做这道题我大概需要这些变量：

在汇编语言中，对于单个变量，例如i/j/k都可以直接用寄存器$t0等，所以只需要对二维数组申请空间，同时由于输出要用到空格和回车，所以也需要对这两个字符申请空间，具体如下：

由于本题我们无法提前得知行数和列数，因此只能用题目给的范围的最大值进行定义，即定义8 * 8的范围。
2. 数据的读取
数据的读取分为两个部分，首先就是对具体行数列数的读入，用一个简单的syscall 读入就好：

由于本题的行列数需要长期使用，所以将其存入s寄存器，放在$s0中随时取用。

然后就是对二维数组一个一个读取放入，此时可以首先定义一个寻找地址的宏：

需要注意，本题由于圈定的范围是8 * 8而不是n * n，所以数据的地址获取是i * 8 + j而非i * n + j，否则就完全错误了。

数据的读入就是利用一个简单的循环嵌套，C语言的写法大概是：

将其翻译成汇编语言就好，利用beq指令进行判断本行/列是否完成输入并进行跳转。

3. 数据运算并存入输出二维数组
   矩阵的乘法其实就是，将第一个矩阵的第i行的所有元素和第二个矩阵第j列所有元素分别相乘后相加，再存入输出矩阵的[i][j]位置就好。所以此处再添加一个k变量进行三重循环就好，和读取的方式很像，仅展示计算处汇编代码：

4. 运算后的结果数组输出
   和读入几乎完全一致，只是把sw指令换成lw指令，不再赘述。

P2.Q2 回文串判断

• 题面

实现满足下面功能的汇编程序：
判断输入的字符串是不是回文串，输出一个字符，是回文串输出1，否则输出0。

输入格式：
第一行为一个整数n，代表字符串的长度。第二行开始的n行：每行一个字符(小写字母)，连起来为输入的字符串。(0<n<=20)

输出格式：
输出为一行，输出一个字符，是回文串输出1，否则输出0。

• 注意事项

1. 如果你采取每次读入一个字符的系统调用（$v0=12）来读入数据,那么我们保证你不会读入到任何换行符。如果你采取这种方式输入，那么对于样例，你可以在MARS中首先手动输入5，打回车，然后手动在一行之中输入abbdl。
2. 如果你采取一次读一行的系统调用（$v0=8），那么你读入的每行有一个小写字母以及行尾的一个换行符。
3. 请使用syscall结束程序。

• 思路
  大致的C语言思路如下，进行翻译：

首先进行数据的空间申请，本题需要申请的只有存放字符的数组，也不需要对空格或回车做出说明。

然后读入两个量，首先是需要读入的字符数，利用$s1进行存储，然后是判断是否还是回文串的标志变量（相当于flag），利用$s0进行存储。

之后的读入和第一题类似，但是一维数组更简单，只需要把循环量乘4就是地址（利用word申请肯定如此）。

至于进行判断，其实就是对于i和n-i-1两个对称元素进行判断就可以，可以利用i<n/2进行范围缩小（只需要保证前半段可以一一匹配后半段就可以）
需要注意的是，我们只能在不相等的时候给$s0赋值1，而不能在相等的时候再赋值0，因为要保证全部相等，如果这么做只要保证最后一次是相等就能判断成功，很明显是不正确的，因此要注意条件语句的写法。

此处展示判断语句的写法：

最后直接输出$s0并且syscall结束即可，不再赘述。

P2.Q3 卷积运算

• 题面

使用MIPS汇编语言编写一个进行卷积运算的汇编程序。
卷积运算的定义：

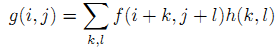
其中f为待卷积矩阵，h为卷积核，g即为输出矩阵，k与l的终值分别为卷积核h的行大小、列大小。计算中不考虑边缘效应。

具体要求：

1. 首先读取待卷积矩阵的行数m1和列数n1，然后读取卷积核的行数m2和列数n2。
2. 然后再依次读取待卷积矩阵(m1行n1列)和卷积核(m2行n2列)中的元素。
3. 卷积核的行列数分别严格小于待卷积矩阵的行列数.
4. 测试数据中0<m1, n1, m2, n2 <11
5. 输入的每个数的绝对值不超过2^10.
6. 最终输出进行卷积后的结果
7. 输出中，有m1-m2+1行，每行有n1-n2+1个数据，每个数据用空格分开。
8. 请使用syscall结束程序。

• 样例

输入：
4 3 2 2 1 2 3 4 5 6 7 8 9 10 11 12 0 1 2 3（空格全都是换行符，此处为了节省空间不展示）
输出：
25 31
43 49
61 67

• 思路

先看一下用C语言表示的代码吧：

给数组申请空间也是和第一题比较类似，注意申请的时候要初始化0，也即要用“.word 0:100”的格式，如下：

可以发现，输入输出和第一题都没有什么差距，可能唯一的差距在于，由于本题的矩阵范围是小于等于10，因此用宏求地址时不是乘8而是乘10，如下：

剩下的其实没有什么可以说的，主要是中间的四重循环要小心点写。尤其是我使用了一个all来当作输出矩阵每一个元素的输入值，因此要注意这个寄存器的清零和放入都是在第二层循环中放入的（i,j循环，k,l未循环）（观察C语言也可以发现）
其余的和第一题矩阵乘法并没有差别，不再赘述。下面是四层循环最中间的计算部分：

P2.Q4 全排列生成

• 题面

实现满足下面功能的汇编程序：

1. 使用mips实现全排列生成算法。
2. 以0x00000000为数据段起始地址。
3. 输入一个小于等于6的正整数，求出n的全排列，并按照字典序输出。
4. 每组数据最多执行500,000条指令。
5. 请使用syscall结束程序。

输入格式：
只输入一行，输入一个整数n (0<n<=6)

输出格式：
按照字典序输出n!行数组，每行输出n个数字，数字之间以空格隔开，每行最后一个数字后可以有空格。

• 样例：

输入：
4
输出：
1 2 3 4
1 2 4 3
1 3 2 4
1 3 4 2
1 4 2 3
1 4 3 2
2 1 3 4
2 1 4 3
2 3 1 4
2 3 4 1
2 4 1 3
2 4 3 1
3 1 2 4
3 1 4 2
3 2 1 4
3 2 4 1
3 4 1 2
3 4 2 1
4 1 2 3
4 1 3 2
4 2 1 3
4 2 3 1
4 3 1 2
4 3 2 1

• C代码提示：

• 思路：

带有递归算法的汇编语言是真的麻烦……这里需要的就是细心。首先，由于需要对每次递归的参数进行保护，所以需要频繁执行入栈、出栈操作，此时可以写push和pop函数来简便算法。（本题开始的存储空间申请部分略去）

其实要注意的主要就是对函数中何时应该入栈、出栈，何时应该跳转进入下一层。虽然和华哥交流的时候，他推荐把除了ra以外的出入栈操作都写在下一层函数前后，相当于上一层函数对数据进行保护，如下：

但我还是觉得这种方式不够直观，毕竟这种方式把ra的出入栈和其他临时变量的出入栈分离了，写起来比较要动脑子。我喜欢的还是在下一层函数的开头进行入栈，结束进行出栈。这种方式的写法是完全固定的：在函数开始时就全部入栈，然后在后面只要遇到return，或者函数结束，就进行出栈，也不用考虑ra的特殊性，出完栈直接jr回ra存储的地址即可（完全不用考虑调用函数的时候的出入栈，因为不需要，调用下一层函数直接调用就可以，只是要传参，如上图未注释部分）。

入栈+传参：

两处出栈：

（好像没什么好说的，就是return处写一个，结尾处也写一个，不要忘了结尾处，不然只要到结尾就回主函数了 ）

还有一些细节：

1. 入栈和出栈的寄存器顺序应该是正好相反的，这样才能够保证出栈的寄存器还原的数据是入栈的自身的数据，而不是入栈的其他寄存器的数据。
2. 本题考虑到a0需要在函数中做输出时输出数据的存储寄存器来syscall，所以利用了a1寄存器进行传参。所以本题a1是不需要出入栈的，因为保证a1只有传参用途，只在相邻的上下两层函数中连接，不需要返回旧状态；反之，a0则需要入栈，因为本题a0在函数中起到了输出作用，是一个临时变量，因此需要出入栈。
3. 调试的时候用2调试看能不能出1 2 2 1就可以了，用4太难了。

输出（其实和前面的输出几乎一致，就是翻译C代码）：

P2.Q5 01迷宫

• 题面

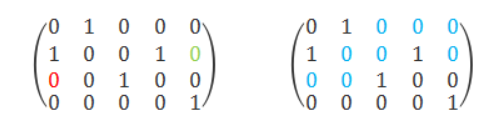
1. 左图表示的是一个4 * 5的01矩阵，这个矩阵就是一个01迷宫。
2. 如左图，以红色0作为起点，绿色0作为终点，每一次行进只能选择上下左右中值为0且未走过的位置，满足上述条件的路线，即为一条迷宫逃跑路线。如右图中，蓝色的路线即为一条逃跑路线。
3. 使用mips实现01迷宫路线数目计算。
4. 以0x00000000为数据段起始地址。
5. 输入一个n * m的01矩阵作为01迷宫，并给定他的起点与终点，求出他不同逃跑路线的数目（不同逃跑路线中可以有相同的部分，但是不能完全相同）。

输入格式：
前两行输入两个整数n和m（n、m均为正整数并且小于等于7），分别代表01矩阵行数和列数。接下来的n * m行，每行输入1个整数（0或1），对应着01矩阵各个元素值(第i * m+j个整数为矩阵的第（i+1）行第j个元素，即一行一行输入)。接下来的四行分别代表迷宫的起点和终点，每行一个整数，分别代表起点与终点行数和列数。

输出格式：
只输出一个整数，代表逃跑路线的数目。

样例输入：
4 5 0 0 1 0 0 1 0 0 0 1 1 0 1 0 1 1 0 0 0 0 1 1 4 5（空格都是回车，为了节省空间进行了修改）
样例输出：
2

• 思路：
  本题的解决方法其实也是一个递归调用。我的思路是：一开始将一个9 * 9矩阵全部赋值为1，然后后面将中间的7 * 7的部分按题目意思分别赋0或1。其原因是，最后的起点终点表示是从1开始的。如果是（1，1），我们就不需要转化为（0，0）再进行输出。
  还有一个好处是：我的寻路思路是，先把当前位置赋值为1，然后向上下左右四个方向进行查找，如果是0，就进入那个方向的下一个格子。当四个方向都探索完成后，再把本格赋值改回0。如果本格就是终点就把逃跑路线数加一。所以为了保证四个方向都依然在我们的矩阵中，所以要给原本是7 * 7的矩阵”包一圈1“，这样就不用进行边界判断了。
  （顺便一提，我一开始写成8 * 8了，只包了左上两个方向，最终果然tle了）
  给出我的C代码：

  #include<stdio.h>
  int map[9][9];
  int routes = 0;
  
  void getRoad(int x,int y,int outx,int outy){
  	if(x==outx&&y==outy){
  	    routes++;
  	    return;
  	}
  	else{
  		map[x][y]=1;
  		if(map[x-1][y]==0)
  		    getRoad(x-1,y,outx,outy);
  		if(map[x][y-1]==0)
  		    getRoad(x,y-1,outx,outy);
  		if(map[x+1][y]==0)
  		    getRoad(x+1,y,outx,outy);
  	    if(map[x][y+1]==0)
  	        getRoad(x,y+1,outx,outy);
  	    map[x][y]=0;
  	    return;
  	}
  }
  
  int main(){
  	int i,j,n,m,input;
  	int inx,iny,outx,outy;
  	for(i=0;i<9;i++)
  	    for(j=0;j<9;j++)
  	        map[i][j]=1;
  	scanf("%d",&n);//行数 
  	scanf("%d",&m);//列数
  	for(i=0;i<n;i++)
  	    for(j=0;j<m;j++){
  		    scanf("%d",&input);
  			map[i+1][j+1]=input;
  		}//输入真正的0-1
      scanf("%d",&inx);
  	scanf("%d",&iny);
  	scanf("%d",&outx);
  	scanf("%d",&outy); 
  	getRoad(inx,iny,outx,outy);
  	printf("%d",routes);
  	return 0;
  }

  一旦检测C语言没有太大问题，那么我们进行转化即可。有几个点需要注意：
  首先是二维矩阵寻址的写法：

这里想要强调的是：一定要在乘法的时候把9赋给一个空寄存器。我一开始是把它赋给了%ans，然后就发现因为后面我有getindex(%t2,%t2,%t1)这样的语句，我们就提前把本来应该作为行数的x也赋成了9，就会出错。

矩阵的置1和输入都和前面的操作类似，没什么特别的，略过。
其次就是最恶心的递归函数的写法。（我们首先忽略出入栈的问题）首先考虑的是其是否到达终点。我的思路就是分别判断行列数是否相等，行数相等就给一个寄存器置1，列数同样。这样这两个寄存器之和为2时，证明到达了重点。如图：

然后就是当没有到终点时，先对本格置1，然后进行四周的探索，最后本格置0。操作如下：

（这个是开头的置1和一个方向的探测递归）

最后就是考虑出入栈的问题：
我的出入栈写法都是在本函数开始的时候进行入栈，最后在本函数结束（return或者最后）进行出栈。这相当于在被调用函数的前后进行维护。当然华哥跟我说在调用下一层函数的开始时入栈，结束时出栈也是可以的。但是我还是觉得我这种方法最好，因为不用脑子。
顺便，对于这题，在没有到终点是对本格先置0后置1，这其实也是一种出入栈的维护。
没到终点的出栈如下：

记得入栈和出栈要进行顺序上的一一对应。

P2.Q6 高精度阶乘

• 题面
  使用MIPS汇编语言编写一个求n的阶乘的汇编程序(不考虑延迟槽)。
  具体要求：

1. 第一行读取n
2. 计算并输出n的阶乘，输出字符串长度小于等于1000
3. 步数限制为200,000
4. 请使用syscall结束程序

样例输入：
24
样例输出：
620448401733239439360000

• 思路
  首先先写出C语言代码：

  #include<stdio.h>
  int main(){
  	int n,out[1000]={1},i,j;
  	int high=1,up;
  	scanf("%d",&n);
  	for(i=2;i<=n;i++){
  		up=0;
  		for(j=0;j<high;j++){
  		    out[j]=i*out[j]+up;
  		    up=out[j]/10;
  		    out[j]%=10;
  		}
  		while(up){ //最高位 
  			out[high]=up%10;
  			high++;
  			up/=10;
  		}
  	}
  	for(i=high-1;i>=0;i--)
  	    printf("%d",out[i]);
  	return 0;
  }

  这里主要就是要领悟乘法的本质。例如123 * 12，其真正的计算方法就是“1”，“2”，“3”这三位分别乘以12再加上进位。所以我们将out数组中从低到高分别乘新数加进位就是这一位新的值。这就是out[j]=i*out[j]+up;的意思，之后还要进行一次进位的计算处理。还有要注意，当阶乘足够大的时候，其进位可能很大，所以对于最高位我们不能只处理一次up%10作低位，up/10做高位的操作，而应该进行一个循环，如果进位占满高一位（up/10!=0）时要继续处理，所以要进行一个while循环。

将其转换到mips中即可：

这里是对于每一位的计算存储。

然后这里是对最高位残留的up进行处理，确保高位正确。
最后进行循环输出就可以，略过。
注意：目前为止，我的汇编代码没有办法处理0的阶乘！（甚至不能纳入循环，因为我默认至少是2开始乘，1直接输出），所以最后就写了个如果输入是0直接跳转到输出1的beq，并把输出附在了最后。

还有一个注意：开头的时候我们的数组是全零的，这个时候无法进行乘法，需要把第一位置成1才能开始阶乘运算，也就是int out[1000] = {1}

以上就是P2的全部题目，由于校庆少了一周上机，我也许现在就要考虑P3的搭CPU了，又怕P2过不了，烦呐。