线性代数
对于一个标量a ∈ N a \in N a ∈ N
简单操作,例如c = a + b c = a + b c = a + b c = a ⋅ b c = a \cdot b c = a ⋅ b c = sin a c = \sin a c = sin a
长度判定,对于一个标量,可以将其长度理解为:
∣ a ∣ = { a , i f a > 0 − a , o t h e r w i s e |a| = \begin{cases} a \space ,\space if \space a > 0
\\ -a \space , \space otherwise \end{cases}
∣ a ∣ = { a , i f a > 0 − a , o t h er w i se
同时对于一个标量的长度,还有以下结论:
∣ a + b ∣ ≤ ∣ a ∣ + ∣ b ∣ |a + b| \leq |a| + |b|
∣ a + b ∣ ≤ ∣ a ∣ + ∣ b ∣
∣ a ⋅ b ∣ = ∣ a ∣ ⋅ ∣ b ∣ |a \cdot b| = |a| \cdot |b|
∣ a ⋅ b ∣ = ∣ a ∣ ⋅ ∣ b ∣
对于一个向量a ∈ N m a \in N^m a ∈ N m
c = a + b , w h e r e c i = a i + b i (向量逐元素相加) c = a + b \space , \space where \space c_i = a_i + b_i (向量逐元素相加)
c = a + b , w h ere c i = a i + b i (向量逐元素相加)
c = α ⋅ b , w h e r e c i = α b i (向量乘标量) c = \alpha \cdot b \space , \space where \space c_i = \alpha b_i (向量乘标量)
c = α ⋅ b , w h ere c i = α b i (向量乘标量)
c = sin a , w h e r e c i = sin a i (向量逐元素求正弦) c = \sin a \space , \space where \space c_i = \sin a_i (向量逐元素求正弦)
c = sin a , w h ere c i = sin a i (向量逐元素求正弦)
对一个向量,其长度被定义为元素平方和开根号:
∥ a ∥ 2 = ∑ i = 1 m a i 2 \|a\|_2 = \sqrt{\sum^{m}_{i=1}a^2_i}
∥ a ∥ 2 = i = 1 ∑ m a i 2
同时对于一个向量,其长度也有以下结论:
∥ a ∥ ≥ 0 , f o r a l l a (所有向量长度均为非负值) \|a\| \geq 0 \space , \space for \space all \space a (所有向量长度均为非负值)
∥ a ∥ ≥ 0 , f or a ll a (所有向量长度均为非负值)
∥ a + b ∥ ≤ ∥ a ∥ + ∥ b ∣ (三角形法则,向量相加后长度小于各向量长度相加) \|a + b\| \leq \|a\| + \|b| (三角形法则,向量相加后长度小于各向量长度相加)
∥ a + b ∥ ≤ ∥ a ∥ + ∥ b ∣ (三角形法则,向量相加后长度小于各向量长度相加)
∥ α ⋅ b ∥ = ∣ α ∣ ⋅ ∥ b ∥ (向量数乘后的长度等于其长度乘以标量绝对值,相当于延长或反向延长) \|\alpha \cdot b\| = |\alpha| \cdot \|b\| (向量数乘后的长度等于其长度乘以标量绝对值,相当于延长或反向延长)
∥ α ⋅ b ∥ = ∣ α ∣ ⋅ ∥ b ∥ (向量数乘后的长度等于其长度乘以标量绝对值,相当于延长或反向延长)
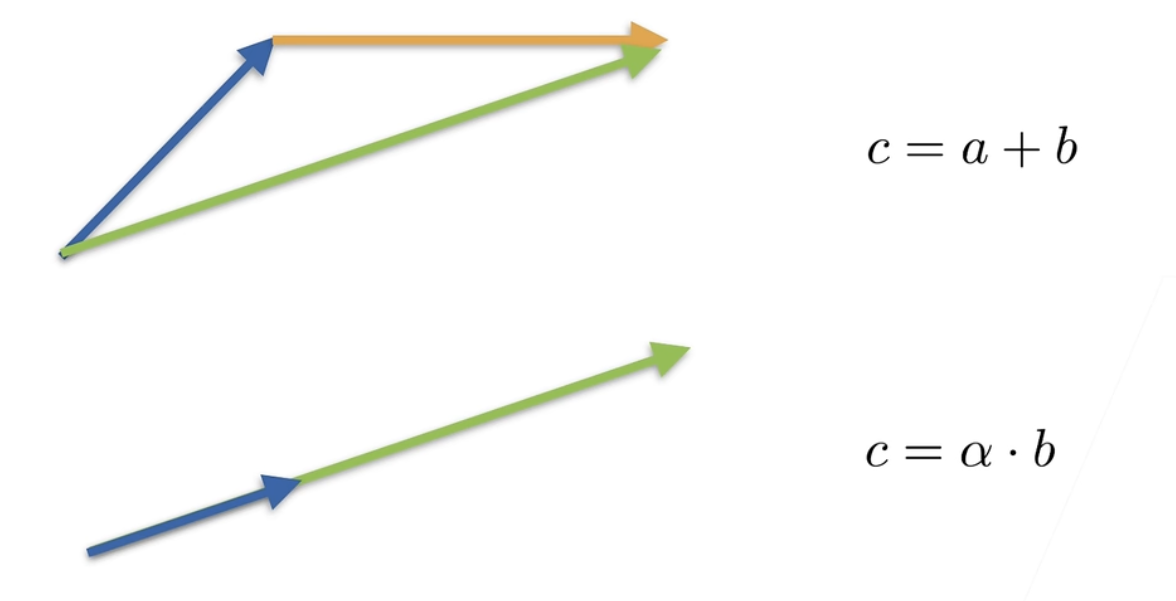
向量运算的直观理解如下图所示:
a ⋅ b = a ⊤ b = ∑ i a i b i a \cdot b = a^{\top}b = \sum_{i}a_ib_i
a ⋅ b = a ⊤ b = i ∑ a i b i
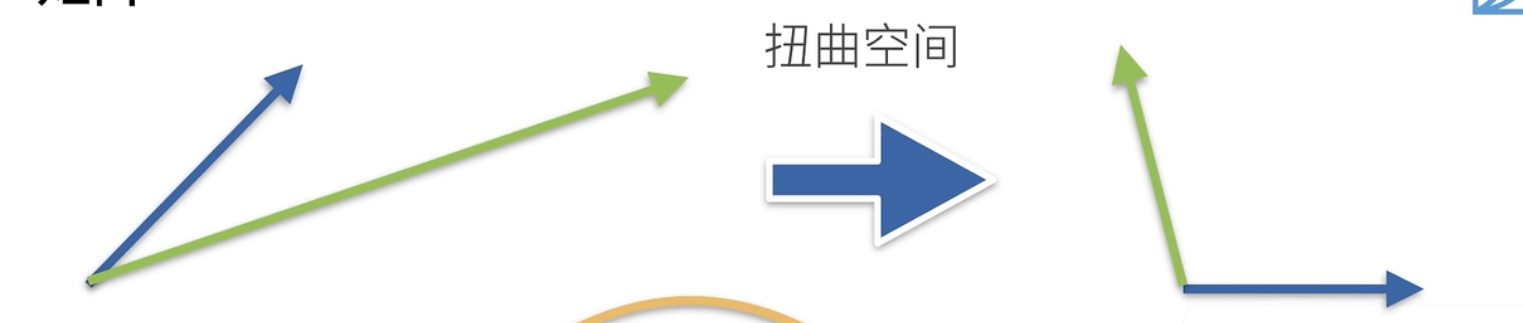
当两个向量正交(垂直)时,其点乘结果为0:
a ⋅ b = a ⊤ b = ∑ i a i b i = 0 (当两向量正交时) a \cdot b = a^{\top}b = \sum_{i}a_ib_i = 0 (当两向量正交时)
a ⋅ b = a ⊤ b = i ∑ a i b i = 0 (当两向量正交时)
矩阵A ∈ N m × n A \in N^{m \times n} A ∈ N m × n
C = A + B , w h e r e C i j = A i j + B i j (矩阵逐元素相加) C = A + B \space , \space where \space C_{ij} = A_{ij} + B_{ij} (矩阵逐元素相加)
C = A + B , w h ere C ij = A ij + B ij (矩阵逐元素相加)
C = α ⋅ B , w h e r e C i j = α B i j (矩阵乘标量) C = \alpha \cdot B \space , \space where \space C_{ij} = \alpha B_{ij} (矩阵乘标量)
C = α ⋅ B , w h ere C ij = α B ij (矩阵乘标量)
C = sin A , w h e r e C i j = sin A i j (矩阵逐元素求正弦) C = \sin A \space , \space where \space C_{ij} = \sin A_{ij} (矩阵逐元素求正弦)
C = sin A , w h ere C ij = sin A ij (矩阵逐元素求正弦)
矩阵和向量的乘法需要注意矩阵每行的元素数(维度)要等于向量的元素数(维度),或若将向量也看作矩阵,可以认为左侧矩阵的列数需等于右侧矩阵的行数:
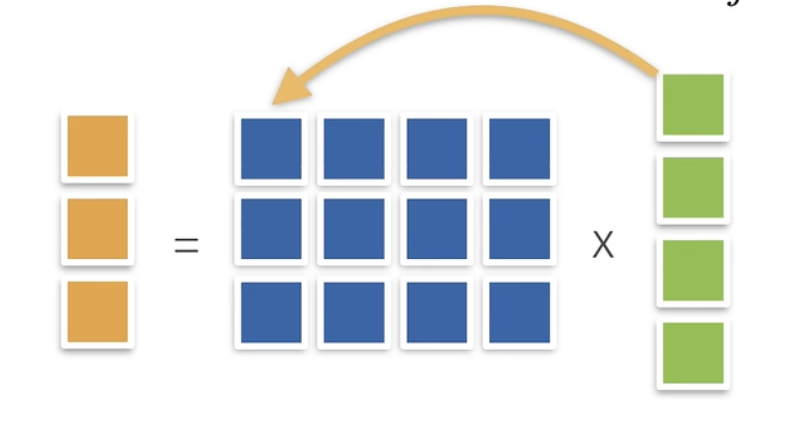
c = A b , w h e r e c i = ∑ j A i j b j c = Ab \space , \space where \space c_i = \sum_{j} A_{ij}b_j
c = A b , w h ere c i = j ∑ A ij b j
其具体乘法过程如下图所示:
矩阵和矩阵的乘法相当于矩阵和向量的乘法的合并,其要求同样为可以认为左侧矩阵的列数需等于右侧矩阵的行数:
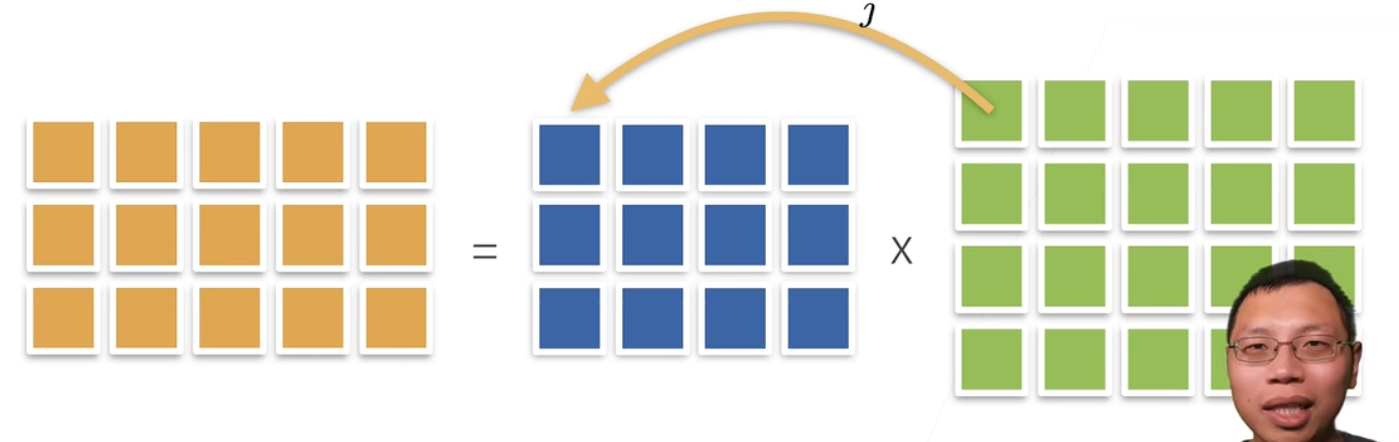
C = A B , w h e r e C i k = ∑ j A i j B j k C = AB \space , \space where \space C_{ik} = \sum_j A_{ij}B_{jk}
C = A B , w h ere C ik = j ∑ A ij B jk
其具体过程如下图所示:
矩阵还有范数概念。我认为范数概念相当于向量的长度概念的引申,都是将一个多元素的对象映射为一个标量。然而对于一个矩阵,其范数定义可以是多样的(映射到标量的方法多样),由于有:
c = A ⋅ b h e n c e ∥ c ∥ ≤ ∥ A ∥ ⋅ ∥ b ∥ c = A \cdot b \space hence \space \|c\| \leq \|A\| \cdot \|b\|
c = A ⋅ b h e n ce ∥ c ∥ ≤ ∥ A ∥ ⋅ ∥ b ∥
可以定义的范数包括:
矩阵范数:最小的满足上式的值即为∥ A ∥ \|A\| ∥ A ∥
F范数(一般使用):可以理解为将矩阵所有对象取出并填入一个向量后向量的长度。如下图:
∥ A ∥ F r o b = ∑ i j A i j 2 \|A\|_{Frob} = \sqrt{\sum_{ij}A^2_{ij}}
∥ A ∥ F ro b = ij ∑ A ij 2
一些特殊的矩阵特质:
对称:即主对角线两侧元素相等。判定式:A i j = A j i A_{ij} = A_{ji} A ij = A ji
反对称:即主对角线两侧元素分别为相反数。判定式:A i j = − A j i A_{ij} = -A_{ji} A ij = − A ji
正定:即对于任意向量x x x x ⊤ A x ≥ 0 x^{\top}A x \geq 0 x ⊤ A x ≥ 0
正交矩阵:所有行都相互正交,所有行都为单位长度,判别为:U U ⊤ = E UU^\top = E U U ⊤ = E
置换矩阵:每行、每列中恰好只有一个元素为1,其余元素均为的矩阵。即:P w h e r e P i j = 1 i f a n d o n l y i f j = π ( i ) P \space where \space P_{ij} = 1 \space if \space and \space only \space if \space j = \pi(i) P w h ere P ij = 1 i f an d o n l y i f j = π ( i )
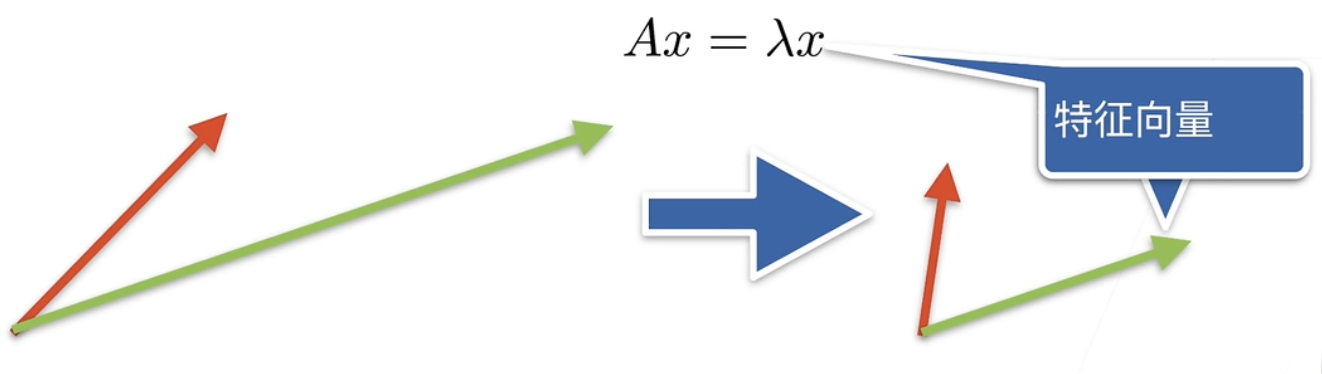
重要概念:特征向量和特征值
其定义为:A x = λ x Ax = \lambda x A x = λ x x x x λ \lambda λ
注意,并非所有矩阵都能找到特征向量。然而,对称矩阵永远可以找到特征向量。
后续线性代数相关概念在Pytorch中的实现见:线性代数实现。
线性代数实现
可以通过生成只有一个元素的张量来表示标量,标量也可以进行基本操作:
1 2 3 4 5 import torch3.0 ])2.0 ])print (x + y, x * y, x / y, x ** y)
向量可以被视为标量值组成的列表,且可以通过张量的索引访问其中的任意元素:
1 2 x = torch.arange(4 )print (x[3 ])
可以获知一个张量的长度及一个张量的形状。由于张量只有一个轴(一维),因此其形状由单个元素表示:
1 2 print (len (x)) print (x.shape)
可以通过首先创建一个张量,再使用数据操作实现中提到的reshape()函数的方式将其转化为一个指定行列数的矩阵:
1 2 3 4 5 6 7 8 9 10 A = torch.arange(20 ).reshape(5 , 4 )print (A)"""输出: tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11], [12, 13, 14, 15], [16, 17, 18, 19]]) """
可以通过代表转置符号的T实现对矩阵的转置(行变列、列变行):
1 2 3 4 5 6 7 8 print (A.T)"""输出: tensor([[ 0, 4, 8, 12, 16], [ 1, 5, 9, 13, 17], [ 2, 6, 10, 14, 18], [ 3, 7, 11, 15, 19]]) """
(可以使用Python测试,一个对称矩阵等于其转置,即A = A ⊤ A = A^\top A = A ⊤
1 2 3 4 5 6 7 8 B = torch.tensor([[1 , 2 , 3 ], [2 , 0 , 4 ], [3 , 4 , 5 ]]) print (B == B.T)"""输出: tensor([[True, True, True], [True, True, True], [True, True, True]]) """
类似向量是标量的推广、矩阵是向量的推广,可以向上构建具有更多轴(更多维度)的数据结构,例如此代码可以构建一个三维数据结构:
1 2 3 4 5 6 7 8 9 10 11 12 X = torch.arange(24 ).reshape(2 , 3 , 4 )print (X)"""输出: tensor([[[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]], [[12, 13, 14, 15], [16, 17, 18, 19], [20, 21, 22, 23]]]) """
(给定具有相同形状的任意两个张量,任何按元素二元运算的结果张量将会与原来的两个张量同形。举例如下)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 A = torch.arange(20 , dtype=torch.float32).reshape(5 , 4 )print (A, A + B)"""输出: tensor([[ 0., 1., 2., 3.], [ 4., 5., 6., 7.], [ 8., 9., 10., 11.], [12., 13., 14., 15.], [16., 17., 18., 19.]]) tensor([[ 0., 2., 4., 6.], [ 8., 10., 12., 14.], [16., 18., 20., 22.], [24., 26., 28., 30.], [32., 34., 36., 38.]]) """
两个矩阵的按元素乘法不同于矩阵相乘,在数学上被称为“哈达玛积”,数学符号为⊙ \odot ⊙
1 2 3 4 5 6 7 8 9 print (A * B)"""输出: tensor([[ 0., 1., 4., 9.], [ 16., 25., 36., 49.], [ 64., 81., 100., 121.], [144., 169., 196., 225.], [256., 289., 324., 361.]]) """
一个标量和一个矩阵的按元素操作,即为该标量和矩阵所有元素执行一次按元素操作。同样,这种操作的结果的形状和输入的矩阵形状依然相同:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 a = 2 24 ).reshape(2 , 3 , 4 )print ((a * X).shape) print (a + X) """输出: tensor([[[ 2, 3, 4, 5], [ 6, 7, 8, 9], [10, 11, 12, 13]], [[14, 15, 16, 17], [18, 19, 20, 21], [22, 23, 24, 25]]]) """
sum()可以计算张量的元素和,也可以被认为是张量降维的一种手段,同时其计算不仅限于一维向量,对于矩阵也可以进行元素和计算:
1 2 print (A.shape) print (A.sum ())
默认情况下求和函数会沿着所有的轴进行加和以降低张量维度,最终变成一个标量;然而还可以通过制定张量沿着哪一个轴求和来降低维度。例如一个矩阵,如果想要通过坍缩第一维的方式进行降维,可以在求和函数中指定轴0(axis=0)。如此,计算之后轴0的维度参数在形状输出中消失,同时,将每一列元素加和(要想理解主要要把握住将指定维坍缩的概念,例如将行坍缩,那么最后生成的矩阵就应该只有一行多列,那么实现这种的方式就是处于同一列的元素相加以压缩,或者说所有行逐元素相加;或者可以考虑压缩前后矩阵的形状和维度会如何改变):
1 2 3 A_sum_axis0 = A.sum (axis=0 )print (A_sum_axis0.shape) print (A_sum_axis0)
同样,也可以指定轴1(axis=1),以通过坍缩第二维(列)进行降维。如此,计算之后轴1的维数在输出形状中消失,同时,将每一行元素加和:
1 2 3 A_sum_axis1 = A.sum (axis=1 )print (A_sum_axis1.shape) print (A_sum_axis1)
如果同时指定轴0和轴1(即对于一个高维张量同时选择加和压缩其所有维度),那么计算后的效果与无参数sum()相同:
1 2 print (A.sum (axis=[0 , 1 ]).shape) print (A.sum (axis=[0 , 1 ]))
一个和求和相关的运算是求均值mean(),当不指定轴时均值即为元素求和结果除元素个数(可以通过numel()或shape()等方式获取);当指定轴时相当于对每一个被压缩的向量进行求均值。示例如下:
1 2 3 4 print (A.mean()) print (A.sum () / A.numel()) print (A.mean(axis=0 )) print (A.sum (axis=0 ) / A.shape[0 ])
使用sum()进行加和时,会进行降维。例如指定轴0,那么原先的第0维(行)就会在加和后消失。可以使用keepdims参数设置,让加和操作不进行降维,即将要压缩的向量求和后存入原向量第一个位置。这样只是相当于将原向量长度缩短为1,而并非将其转化为一个标量,因此其轴数(维数)不会变化:
1 2 3 4 5 6 7 8 9 10 sum_A = A.sum (axis=1 , keepdims=True )print (sum_A)"""输出: tensor([[ 6.], [22.], [38.], [54.], [70.]]) """
不降维的优势是,后续可以使用sum_A与广播机制(见[[数据操作]]),将A和sum_A进行逐元素操作。只要两个张量维数一致就可以操作,然而如果压缩了维度便无论如何不能进行逐元素操作:
1 2 3 4 5 6 7 8 9 print (A /sum_A)"""输出: tensor([[0.0000, 0.1667, 0.3333, 0.5000], [0.1818, 0.2273, 0.2727, 0.3182], [0.2105, 0.2368, 0.2632, 0.2895], [0.2222, 0.2407, 0.2593, 0.2778], [0.2286, 0.2429, 0.2571, 0.2714]]) """
可以使用cumsum()进行累加求和。例如,如果指定轴0,相当于将原0行不动,新1行改为原0行与原1行相加,新2行改为新1行与原2行相加(原1、2、3行相加),以此类推:
1 2 3 4 5 6 7 8 9 print (A.cumsum(axis=0 ))"""输出: tensor([[ 0., 1., 2., 3.], [ 4., 6., 8., 10.], [12., 15., 18., 21.], [24., 28., 32., 36.], [40., 45., 50., 55.]]) """
可以使用dot()实现矩阵(张量)间的点积运算。对于两个同形向量,点积是同位置元素乘积之和(结果是一个标量):
1 2 3 4 x = torch.arange(4 , dtype=torch.float32)4 , dtype=torch.float32)print (x, y) print (torch.dot(x, y))
当然,两个向量点乘也可以使用先按元素相乘再加和的方式实现:
矩阵向量积,即A x Ax A x A A A i i i A A A i i i x x x a i ⊤ x a_{i}^{\top}x a i ⊤ x torch.mv()进行计算:
1 2 3 4 print (A.shape) print (x.shape) print (torch.mv(A, x))
矩阵-矩阵乘法,即A B AB A B B B B A A A A A A B B B torch.mm()计算:
1 2 3 4 5 6 7 8 9 10 B = torch.ones(4 , 3 ) print (torch.mm(A, B))"""输出: tensor([[ 6., 6., 6.], [22., 22., 22.], [38., 38., 38.], [54., 54., 54.], [70., 70., 70.]]) """
向量的L 2 L_2 L 2
∥ x ∥ 2 = ∑ i = 1 n x i 2 \|x\|_2 = \sqrt{\sum^{n}_{i=1}x^2_i}
∥ x ∥ 2 = i = 1 ∑ n x i 2
在pytorch中,可以使用torch.norm计算向量的L 2 L_2 L 2
1 2 u = torch.tensor([3.0 , -4.0 ])print (torch.norm(u))
向量的L 1 L_1 L 1
∥ x ∥ 1 = ∑ i = 1 n ∣ x i ∣ \|x\|_1 = \sum^{n}_{i=1}|x_i|
∥ x ∥ 1 = i = 1 ∑ n ∣ x i ∣
在pytorch中,没有直接求L 1 L_1 L 1 abs()绝对值方法与sum()求和方法结合来求此范数:
1 print (torch.abs (u).sum ())
矩阵中最常用的范数为F F F
∥ X ∥ F = ∑ i = 1 m ∑ j = 1 n x i j 2 \|X\|_F = \sqrt{\sum^m_{i=1}\sum^n_{j=1}x^2_{ij}}
∥ X ∥ F = i = 1 ∑ m j = 1 ∑ n x ij 2
在pytorch中,矩阵的F F F torch.norm进行计算:
1 print (torch.norm(torch.ones((4 , 9 ))))