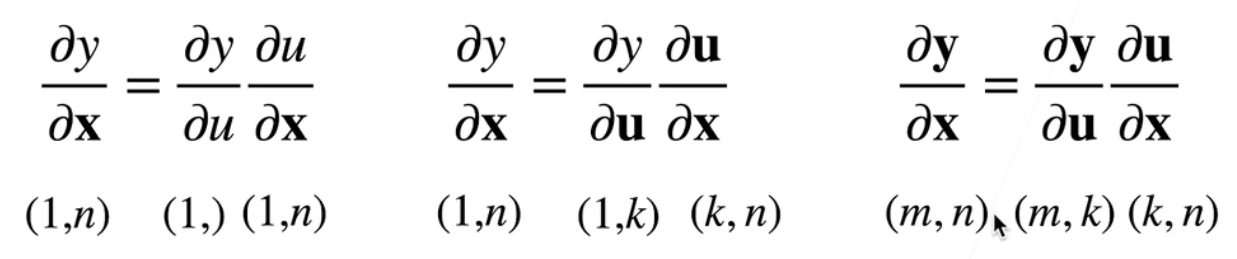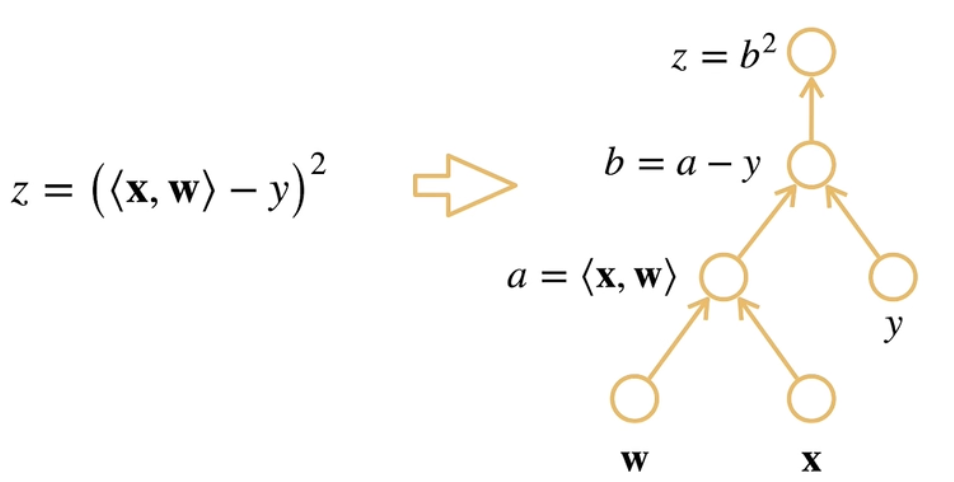矩阵计算
标量导数
| y |
a |
xn |
ex |
logx |
sinx |
u+v |
uv |
y=f(u),u=g(x) |
| dxdy |
0 |
nxn−1 |
ex |
x1 |
cosx |
dxdu+dxdv |
dxduv+dxdvu |
dudydxdu |
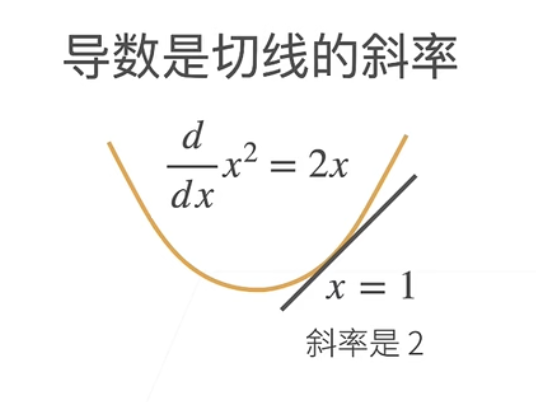
站在几何上的角度来说,导数的几何意义就是原函数切线的斜率:
亚导数
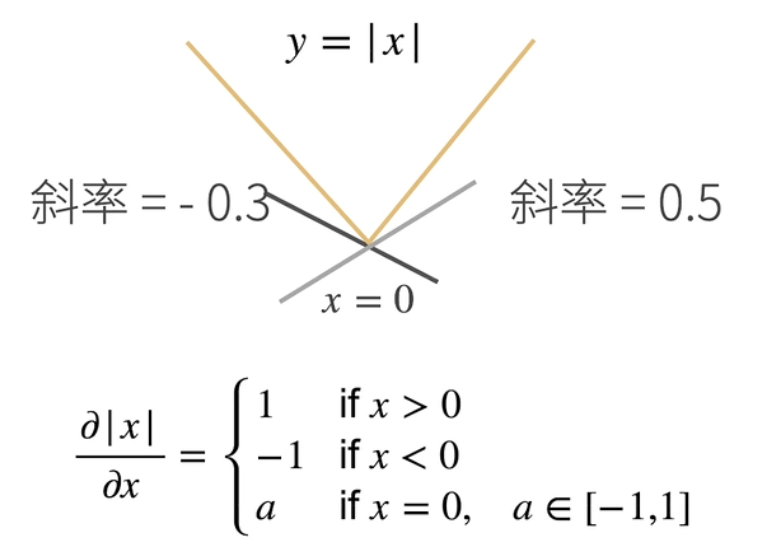
其功能是将导数拓展到不可微的函数上。例如绝对值函数的0点。在绝对值函数0点处,函数的切线斜率不存在或不唯一,此时可以以亚导数形式进行定义:
另外一个例子是与0的取大函数max(x,0),此函数在x<0时恒等于0,而在x≥0时等于x,因此其在x=0时函数不可微,需要用亚导数形式进行表示:
∂x∂max(x,0)=⎩⎨⎧1 , if x>00 , if x<0a , if x=0, a∈[0,1]
梯度
梯度是将标量求导引申至向量求导所得的概念。在将导数拓展到向量时,最重要的是理清求出结果的形状,是标量、向量、亦或是矩阵。具体结果形状如下图:
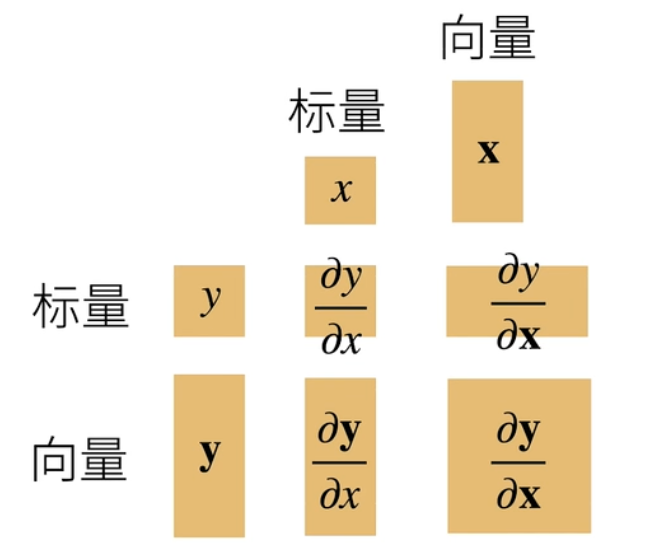
具体分情况讨论如下:
- 当标量对向量求导时(∂x∂y)
当标量对于一个向量求导时,向量为一个列向量,但最后求得的结果向量却是一个行向量:
x=x1x2⋮xn ∂x∂y=[∂x1∂y,∂x2∂y,…,∂xn∂y]
或者可以理解为当标量对向量求导,就是标量对向量组中每一个元素求偏导,再将结果组成一个新的行向量。一个例子如下:
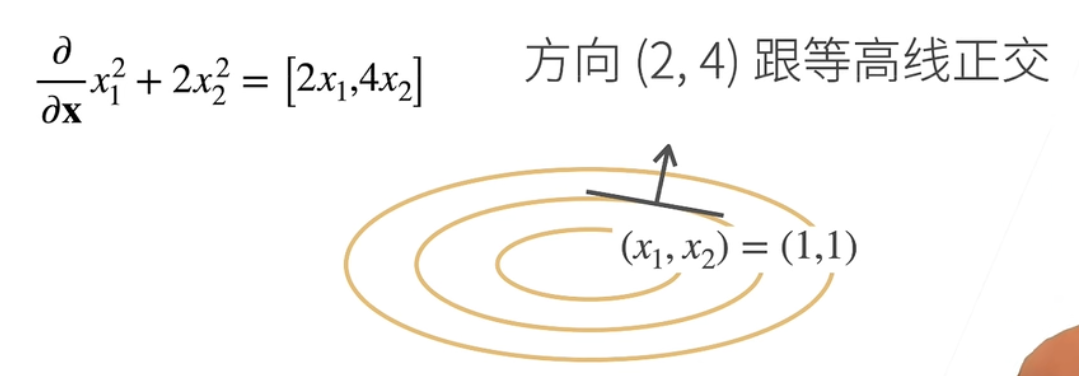
∂x∂x12+2x22=[2x1,4x2]
此求法也可以从几何角度理解:考虑下面这张“等高图”,其中每条线由当y取得同一值时输入的(x1,x2)的取值集合组成。而某一点的梯度,可以看作与该点等高线方向正交的向量方向。也可以说这个方向是会令输出y的值发生最大幅度改变的(x1,x2)改变方向:
不同形式的标量对向量求导汇总如下:
| y |
a |
au |
sum(x) |
∣x∣2 |
u+v |
uv(逐元素相乘) |
<u,v>(内积) |
| ∂x∂y |
0⊤ |
a∂x∂u |
1⊤ |
2x⊤ |
∂x∂u+∂x∂v |
∂x∂uv+∂x∂vu |
u⊤∂x∂v+v⊤∂x∂u |
- 当向量对标量求导时(∂x∂y)
当向量对于一个标量求导时,向量和结果向量都为一个列向量,形状不变(此处和上一节的向量形状规定被称为“分子布局符号”,还可以全部反过来,被称为“分母布局符号”):
y=y1y2⋮ym ∂x∂y=∂x∂y1∂x∂y2⋮∂x∂ym
这种求导方法可以被理解为对向量y中的每一个分量yi,关于标量x求导,然后再合并为一个新同形列向量。
- 当向量对向量求导时(∂x∂y)
当向量对一个向量求导时,结果为一个矩阵,可把这种计算当成上两节所说求导方式的联合运算:
∂x∂y=∂x∂y1∂x∂y2⋮∂x∂ym=∂x1∂y1,∂x1∂y2,⋮,∂x1∂ym,∂x2∂y1,∂x2∂y2,⋮,∂x2∂ym,…,…,…,…,∂xn∂y1∂xn∂y2⋮∂xn∂ym
不同形式的矩阵对矩阵求导汇总如下:
| y |
a |
x |
Ax |
x⊤A |
au |
Au |
u+v |
| ∂x∂y |
0 |
I |
A |
A⊤ |
a∂x∂u |
A∂x∂u |
∂x∂u+∂x∂v |
- 拓展:如果将矩阵也作为输入进行考虑时求导结果形状列举如下:
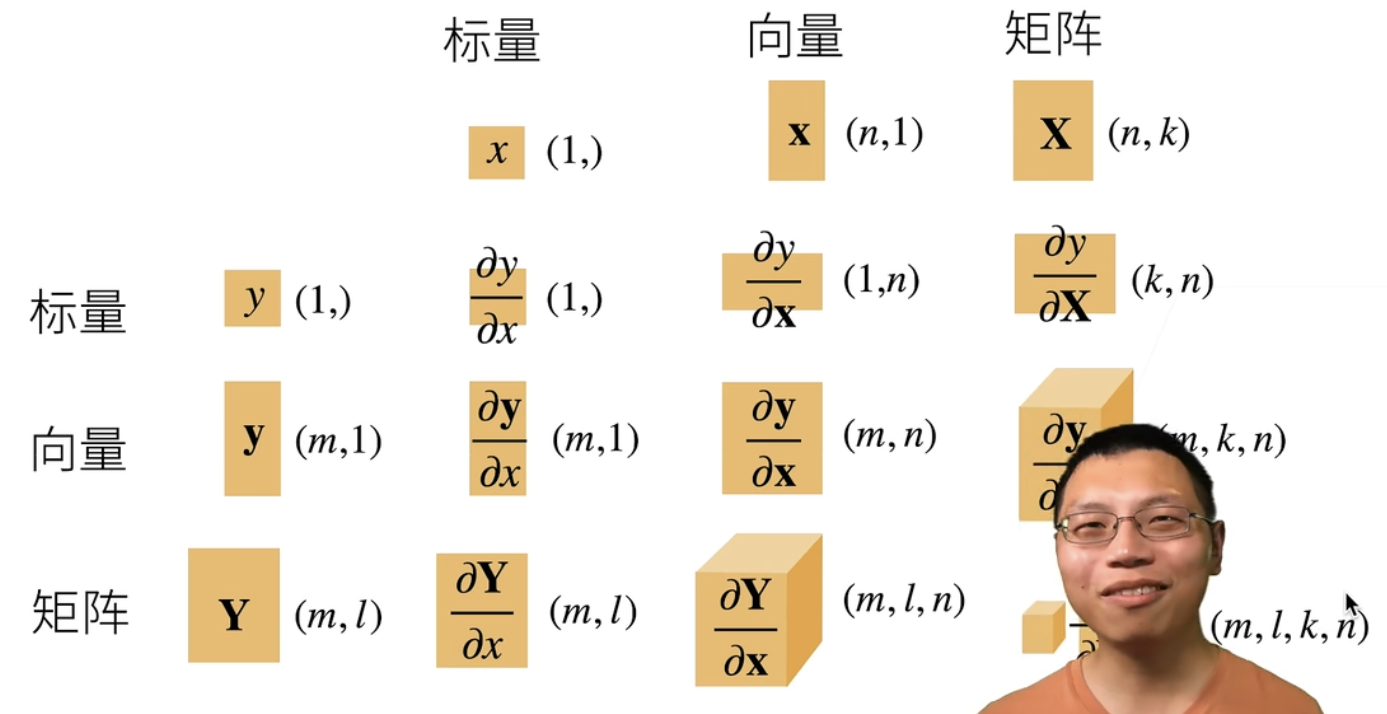
我认为其结果形状的规律是:被求导的对象(y)维度在前,求导的对象(x)维度在后,结果需要合并这两个对象的维度形状,但是对于求导对象x需要先进行转置操作颠倒维度。还要注意对形状为1的维度有时要消除。
自动求导
链式法则
最简单的标量链式法则在矩阵计算中已经提到,格式如下:
y=f(u), u=g(x) ∂x∂y=∂u∂y∂x∂u
但是也正如矩阵计算中提到,向量也是可以作为参与者加入导数运算的。那么如果有向量参与了这种复合函数的链式求导,就需要明白求导过程中各个对象的形状,示意如下(x为n维、y为m维、u为k维向量):
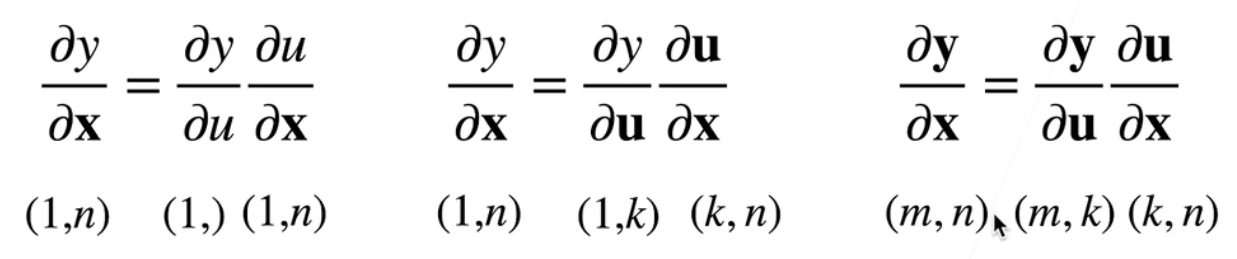
以下为几个计算的例子:
设x, w∈Rn为两个向量,y∈R为标量,z=(<x,w>−y)2,需要计算∂w∂z:
一个简单的方法是可以先进行分解,将复合函数的不同层次用不同参数代替:
a=<x, w>b=a−yz=b2
那么此时,这个复合函数求导就可以被看作:∂w∂z=∂b∂z∂a∂b∂w∂a。然后就可以分层次求导:
∂w∂z=∂b∂z∂a∂b∂w∂a=∂b∂b2∂a∂a−y∂w∂<x,w>=2b ⋅ 1 ⋅ x⊤=2(<x,w>−y)x⊤
注意:∂w∂<x,w>的计算依照了矩阵计算中标量对向量求导时内积的情况。展开如下(以下为我的理解):
∂w∂<x,w>=x⊤∂w∂w+w⊤∂w∂x=x⊤I+w⊤⋅0=x⊤
设X∈Rm×n为m行n列矩阵,w∈Rn为长度为n向量,y∈Rm为长度为m向量,z=∥Xw−y∥2为一个标量,求∂w∂z:
和例1一样,首先可以进行复合函数各部分的分解:
a=Xwb=a−yz=∥b∥2
那么此时这个复合函数也可以进行分层次求导的链式法则了(一些相关导数的展开同样见矩阵计算中的表格):
∂w∂z=∂b∂z∂a∂b∂w∂a=∂b∂∥b∥2∂a∂a−y∂w∂Xw=2b⊤×I×X=2(Xw−y)⊤X
自动求导
自动求导是计算一个函数在指定值上的导数,区别于:
- 符号求导:也就是说给出显式的f(x)与x,最终利用求导法则显式的求出一个∂x∂f(x)的导函数公式
- 数值求导:不知道具体f(x),但可以通过给定的x与微小的h,利用函数值算出某一点的导数值:∂x∂f(x)=limh→0hf(x+h)−f(x)
在pytorch等框架中,实现自动求导使用的是计算图的概念。其操作包括:
- 将代码分解为操作子(类似于之前进行的复合函数部分分解)
- 将计算表示为一个无环图
示意图如下:
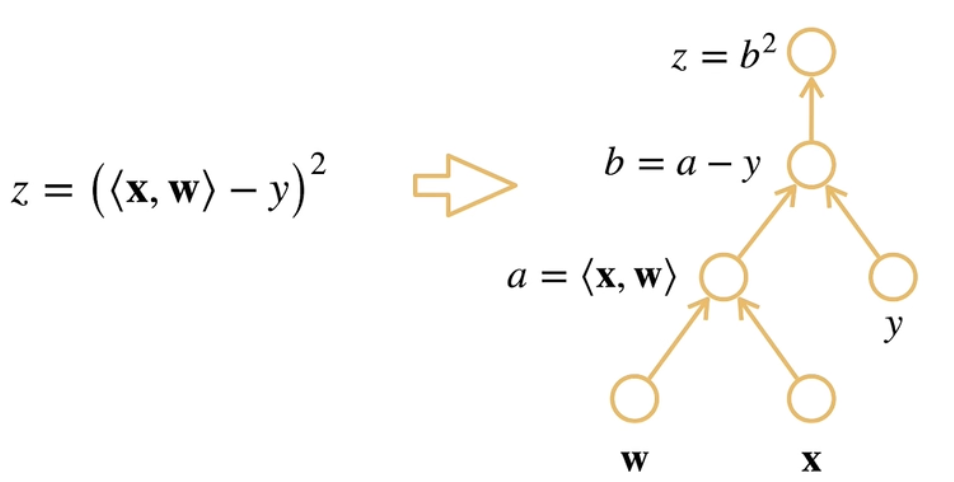
计算图可以进行显示建造,也就是上图中的a,b,c全部都使用代码显示的定义,也可以隐式构造,也就是在计算时不具体重新说明a,b,c的定义(此处理解不是很透彻)
当进行自动求导时,假设使用的链式法则为:∂x∂y=∂un∂y∂un−1∂un…∂u1∂u2∂x∂u1,那么此时有两种方式进行求导:
- 正向累积(计算图自底向上):∂x∂y=∂un∂y(∂un−1∂un(…(∂u1∂u2∂x∂u1)))
- 反向累积、又称反向传递(计算图自顶向下):∂x∂y=(((∂un∂y∂un−1∂un)…)∂u1∂u2)∂x∂u1
反向累积过程示意如下:
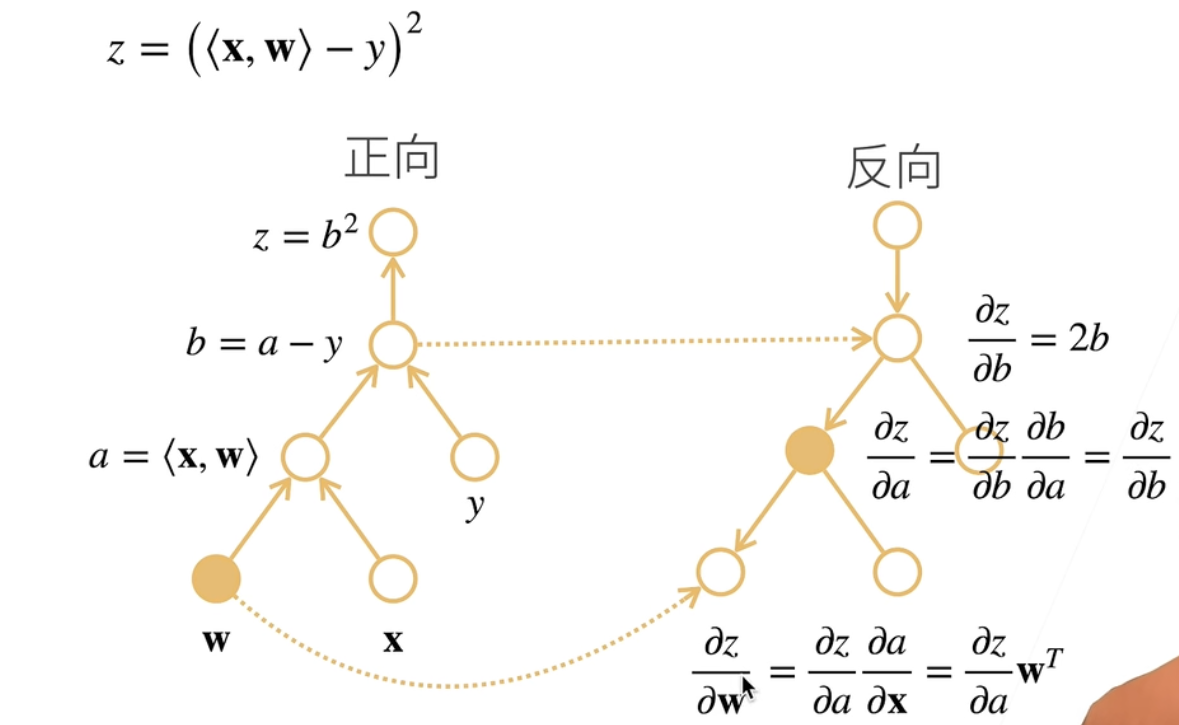
所以一个反向累积的计算过程为:
- 构造计算图
- 进行前向执行:对于每一个节点,存储其相对子节点中间变量进行求导的中间结果
- 进行反向执行:从反方向执行图,同时去除不需要的枝(如果此枝代表的求导计算与结果无关则不进行计算)
反向累积的复杂度分析:
- 计算复杂度为O(n),n代表操作子个数(正向过程所有操作子都要计算一次,反向过程的整个链式法则上的点也要计算一次)
- 内存复杂度为O(n),因为正向过程中所有节点计算的中间结果都需要保存
与之对比,正向累积的计算复杂度同样为O(n)(同样需要计算整个链条上的导数),然而内存复杂度为O(1),因为没有反向累积中的正向过程,不需要保存每个节点的中间结果。然而,正向累积的问题是每次进行计算,即使求导内容不变,也需要重新扫过整个计算图执行正向累积操作。
具体实现见自动求导实现。
自动求导实现
目标:想对函数y=2x⊤x关于列向量x求导。
1
2
3
| import torch
x = torch.arange(4.0)
print(x)
|
- 在计算y对x的梯度之前需要一个地方存储梯度(存储属性为
grad,默认为None):
1
2
| x.requires_grad_(True)
print(x.grad)
|
- 然后可以使用此向量计算y(由于y由隐式构造,因此其会保存和x相关的求导结果):
1
2
| y = 2 * torch.dot(x, x)
print(y)
|
- 后续可以通过反向传播函数来自动计算y关于x每个分量的梯度:
1
2
| y.backward()
print(x.grad)
|
- 如果直接考虑这个函数:x∂2x⊤x=4x⊤,可以验证在
[0, 1, 2, 3]位置的梯度值计算是否正确:
- 现在重新计算x的另一个函数。由于在默认情况下,Pytorch会累积梯度(结果累加),因此在重新计算新梯度之前需要清除之前的梯度计算值后再计算:
1
2
3
4
| x.grad.zero_()
y = x.sum()
y.backward()
print(x.grad)
|
(此处可以理解为:∂x∂[1,1,1,1]x,其结果自然是[1,1,1,1])
- 在深度学习中,求导目的一般不是计算一个微分矩阵,而是批量中每个样本单独计算的偏导数之和(也就是说很少使用向量对向量的求导):
1
2
3
4
5
|
x.grad.zero_()
y = x * x
y.sum().backward()
print(x.grad)
|
- 可以使用
detach()将一些计算移动到记录的计算图之外(视为常数):
1
2
3
4
5
6
7
| x.grad.zero_()
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
print(x.grad == u)
|
- 也可知道,即使是上述情况,
y本身依然是关于x的函数(未被detach),那么其同样可以正确执行对x的求导:
1
2
3
| x.grad.zero_()
y.sum().backward()
print(x.grad == 2 * x)
|
- 即使构建函数的计算图需要经过Python控制流,也可以计算得到变量的梯度(也就是说,在Python感应到计算时就已经将对应的计算图建构完成,后续可以直接求对应梯度),举例如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| def f(a):
b = 2 * a
while b.norm() < 1000:
b = b * 2
if b.sum() > 0:
c = b
else:
c = 100 * b
return c
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
print(a.grad == d / a)
|