学习D2L深度学习课程4:线性回归与线性回归实现

线性回归概念

线性回归模型

对于线性回归，首先观察一个简化的模型例子（买房）：

假设1：影响房价关键因素为卧室个数、卫生间个数、居住面积，记为 $x_1,x_2,x_3$
假设2：成交价是关键因素加权和： $y = w_1x_1 + w_2x_2 + w_3x_3 + b$ ，其中的权重 $w_i$ 与偏差 $b$ 的具体值后续再确定

进行抽象提炼后的线性模型概念如下：

给定一个n维输入 $\textbf{x} = {\begin{bmatrix}x_1, x_2, \dots, x_n \end{bmatrix}}^\top$
线性模型有一个n维权重参数 $\textbf{w} = {\begin{bmatrix}w_1, w_2, \dots, w_n \end{bmatrix}}^\top$ 和一个标量偏差 $b$
最终的输出是输入的加权和： $y = w_1x_1 + w_2x_2 + \dots + w_nx_n + b = <\textbf{w}, \textbf{x}> + b$

线性模型也可以被视作单层神经网络。

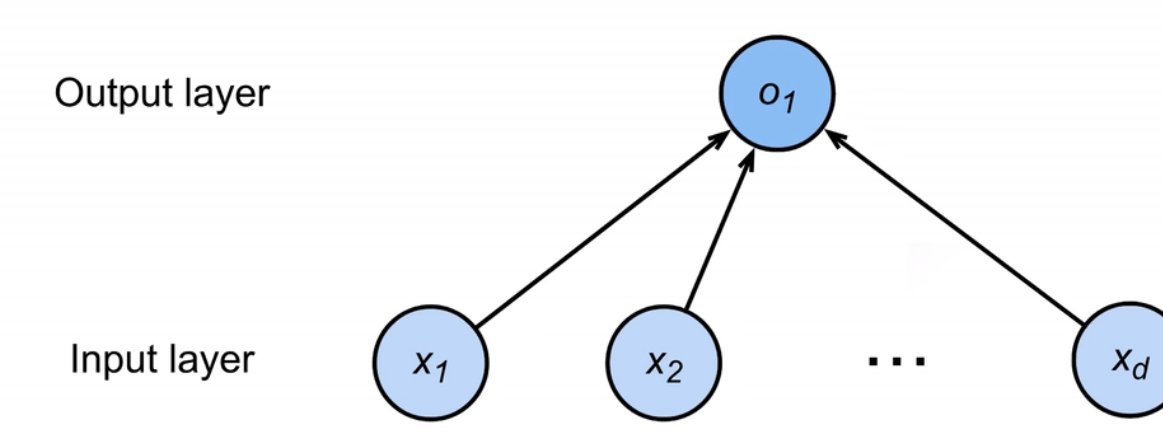
有了这样一个线性模型，就可以对输入进行预估，在预估后，也可以衡量预估质量：也就是说，需要比较真实值和预估值，来衡量目前的模型导致的预估偏差。

举例：设 $y$ 是真实值， $\hat{y}$ 是估计值，则可以比较 $\ell(y, \hat{y}) = \frac{1}{2}(y - \hat{y}) ^2$ ,求得的偏差估计被称作平方损失。

在拥有了模型及损失函数后，就可以收集数据点对模型进行训练，以确定参数值。这些数据被称为训练数据，通常越多越好。假设有n个样本，可以被记为：

\begin{split} & \textbf{X} = {\begin{bmatrix}\textbf{x}_1, \textbf{x}_2, \dots, \textbf{x}_n \end{bmatrix}}^\top \space \space (输入数据点) \\ & \textbf{Y} = {\begin{bmatrix}y_1, y_2, \dots, y_n \end{bmatrix}}^\top \space \space (输出数据点) \end{split}

根据数据集和损失函数的表示，可以符号化当前具体的训练损失（单点损失函数均值）：

\ell(\textbf{X}, \textbf{y}, \textbf{w}, b) = \frac{1}{2n}\sum^n_{i=1} (y_i - <\textbf{x}_i, \textbf{w}> - b)^2 = \frac{1}{2n} \|\textbf{y} - \textbf{X}\textbf{w} - b\|^2

所以最终的目标就是找到一组权重 $\textbf{w}$ 和偏差 $b$ ，使上式的损失函数值最小，即通过最小化损失来学习参数：

\textbf{w}^*, b^* = arg \min_{\textbf{w}, b} \ell (\textbf{X}, \textbf{y}, \textbf{w}, b)

此过程可以求出显式解。求解过程如下：

将偏差加入权重（不需要在权重和输入数据点积后再加偏差项），即将输入数据矩阵和权重向量改为：

\textbf{X} \leftarrow \begin{bmatrix} \textbf{X}, 1 \end{bmatrix} \space , \space \textbf{w} \leftarrow \begin{bmatrix} \textbf{w} \\ b \end{bmatrix}

此时，损失函数就可以被表示为：

\ell(\textbf{X}, \textbf{y}, \textbf{w}) = \frac{1}{2n} \|\textbf{y} - \textbf{X}\textbf{w}\|^2

将此损失函数标量值对权重变量 $w$ 求偏导（具体计算方法见[[矩阵计算]]）：

\frac{\partial}{\partial \textbf{w}} \ell(\textbf{X}, \textbf{y}, \textbf{w}) = \frac{1}{n}(\textbf{y} - \textbf{X}\textbf{w})^\top \frac{\partial}{\partial \textbf{w}}(\textbf{y} - \textbf{X}\textbf{w})^\top = \frac{1}{n}(\textbf{y} - \textbf{X}\textbf{w})^\top \textbf{X}

由于损失函数是一个突函数，因此最优解满足偏导数为0的条件（这是唯一有最优解的模型）：

\begin{split} &\frac{\partial}{\partial \textbf{w}} \ell(\textbf{X}, \textbf{y}, \textbf{w})=0 \\ &\Leftrightarrow \frac{1}{n}(\textbf{y} - \textbf{X}\textbf{w})^\top \textbf{X}=0\\ &\Leftrightarrow (\textbf{y}^\top - \textbf{w}^\top\textbf{X}^\top)\textbf{X}=0 \\ &\Leftrightarrow \textbf{w}^\top\textbf{X}^\top\textbf{X} = \textbf{y}^\top\textbf{X} \\ &\Leftrightarrow \textbf{w}^\top = \textbf{y}^\top\textbf{X}(\textbf{X}^\top\textbf{X})^{-1} \\ &\Leftrightarrow \textbf{w} = (\textbf{X}^\top\textbf{X})^{-1}\textbf{X}^\top\textbf{y} = \textbf{w}^* \end{split}

对于线性回归的总结：

线性回归是对n维输入的加权再加偏差的结果
使用平方损失来衡量预测值和真实值的差异
线性回归模型拥有显式最优解（唯一）
线性回归模型可以被看作单层神经网络

基础优化方法

最基础的优化方法为梯度下降法，其工作过程大致为：

挑选一个训练参数的随机初始值 $\textbf{w}_0$
重复迭代参数 $t=1, 2, 3 \dots$ 次，每次修正参数值为：

\textbf{w}_t = \textbf{w}_{t-1} - \eta \frac{\partial\ell}{\partial \textbf{w}_{t-1}}

此方法可以被直观地理解为，每次修正参数，都挑选当前参数所在位置的负梯度方向进行移动（这样可以使损失函数值减小速度最大），而移动的步长参数由（ $\eta$ 学习率）给出。图示如下：

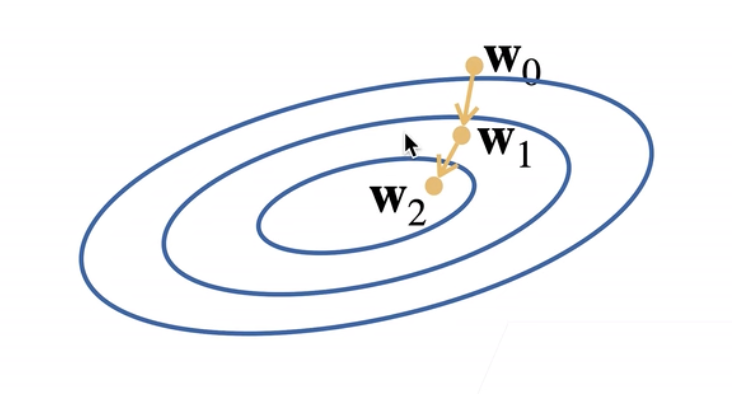
由于 $\eta$ 学习率超参数是人为设定的，因此需要进行合适的选择：不能让训练参数变化步长过小（每次参数修正幅度过小，训练轮次过长，算力消耗过大）或过大（可能会导致损失函数值持续的震荡而非稳定下降）。图示如下：

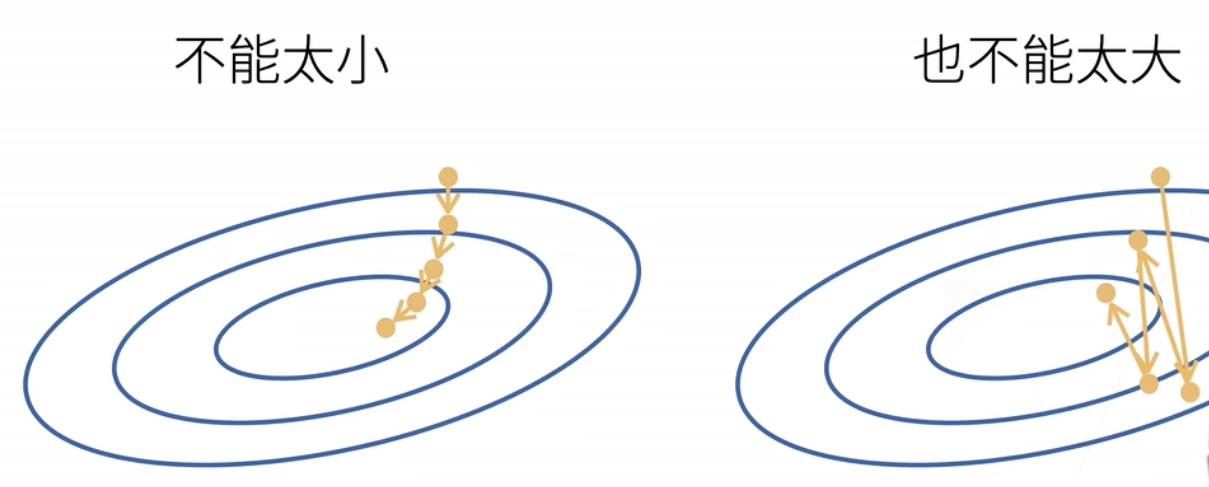
然而这种梯度下降如果在整个训练集上计算会导致算力消耗过大，因为损失函数梯度下降的算力需求和训练集大小（数据个数）线性相关。因此可以采取小批量随机梯度下降的方式。

即，可以对训练集随机采样 $b$ 个样本 $i_1, i_2, \dots, i_b$ ，并只使用这些样本值投入损失函数来近似损失。即此时的损失函数已经缩小变为：

\frac{1}{b}\sum_{i\in I_b}\ell(\textbf{x}_i, y_i, \textbf{w})

此处 $b$ 代表选择样本的批量大小，是另一个人为决定的重要超参数。当批量大小过小时，每次计算量过少，不适合并行以最大利用计算资源；当批量大小过大时，会导致内存消耗增加，且如果出现类似相同样本同时被选取会导致计算资源被浪费。

总结如下：

梯度下降通过不断沿反梯度方向更新参数求解
小批量随机梯度下降是深度学习默认的求解算法
两个重要的超参数是批量大小和学习率

后续线性回归的Pytorch实现见[[线性回归实现]]。

线性回归实现

线性回归基本实现

首先进行一些包的导入，需要random是因为随机梯度下降与参数初始化都需要随机函数：

1
2
3

import random
import torch
from d2l import torch as d2l

然后可以使用一个有噪声的线性模型构造一个人造数据集。此处采用一个权重参数 $\textbf{w} = \begin{bmatrix}2, -3.4 \end{bmatrix}^\top$ ，偏移参数 $b = 4.2$ 与一个随机噪声项 $\epsilon$ 生成的数据集（输入数据 $\textbf{X}$ ）与标签（输出数据 $\textbf{y}$ ）。生成公式为：

\textbf{y} = \textbf{X}\textbf{w} + b + \epsilon

def synthetic_data(w, b, num_examples): # 随机数据生成函数
	X = torch.normal(0, 1, (num_examples, len(w))) # 随机生成输入矩阵
	y = torch.matmul(X, w) + b 
	y += torch.normal(0, 0.01, y.shape) # 利用线性代数公式与噪声项生成对应输出
	return X, y.reshape((-1, 1)) # 将输出整理为一个与输入x对应的列向量（但是轴数为2）

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000) 
# 利用给出的参数和数据量构造数据集和标签

可以通过各种方式查看生成的数据集情况。输出形式为：feature中的每一行包含一个二维数据样本，label的每一行包含一个一维标签值。

print('features:', features[0], ' label:', labels[0]) # 随机查看第一个数据点与标签
# 输出：features: tensor([-0.9650,  0.7661])  label: tensor([-0.3409])

d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1)
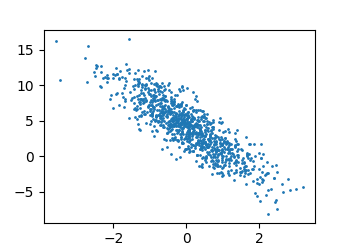
# 查看每一个数据点第一维数据和输出标签的关系图（可以看到线性关系），图像如下：

接下来需要定义一个data_iter函数，这个函数接收批量大小、特征矩阵和标签向量作为输入，生成一个大小为批量大小batch_size的小批量数据。其基本原理就是将整个特征矩阵的每一组特征下标取出并打乱，再按照批量大小分割分次取出一组下标，根据这组下标提取一个小批量的特征和标签值。代码如下：

def data_iter(batch_size, features, labels):
	# 根据输入数据点个数生成一个下标数组并随机打乱
	num_examples = len(features)
	indices = list(range(num_examples))
	random.shuffle(indices)
	# 从打乱的下标数组每次取出批量大小个下标，并根据其取出对应的特征和标签值
	for i in range(0, num_examples, batch_size):
		batch_indices = torch.tensor(
			indices[i:min(i + batch_size, num_examples)])
		yield features[batch_indices], labels[batch_indices]

batch_size = 10
for X, y in data_iter(batch_size, features, labels):
	print(X, '\n', y)
	break
""" 取出的第一个批量组特征矩阵和标签向量情况：
tensor([[ 0.7822,  0.9483],
        [-0.7168, -0.2984],
        [-0.9692,  1.5418],
        [ 1.8321,  0.6736],
        [ 0.5797,  1.3481],
        [ 0.7215,  0.4682],
        [-0.4120,  1.0038],
        [-0.6678, -1.8695],
        [ 0.0059, -0.5556],
        [-1.5461,  0.7406]]) 
 tensor([[ 2.5308],
        [ 3.7727],
        [-2.9753],
        [ 5.5850],
        [ 0.7556],
        [ 4.0652],
        [-0.0372],
        [ 9.2070],
        [ 6.1038],
        [-1.4036]])
"""

在数据设置完成后，需要对模型参数（ $\textbf{w}$ ， $b$ ）进行定义和初始化，同时也需要对模型进行定义：

w = torch.normal(0, 0.1, size=(2, 1), requires_grad=True) 
# w为一行两列矩阵，需要进行梯度下降优化，初始化为期望0方差0.1的随机矩阵
b = torch.zeros(1, requires_grad=True)
# b为标量，需要进行梯度下降优化，初始化为0

def linreg(X, w, b):
""" 线性回归模型位置 """
	return torch.matmul(X, w) + b # 通过指定w和b，输入任何数据集X均可得对应输出y

然后需要定义损失函数（使用均方损失）。为了保险起见，可以通过reshape确保估计值和真知矩阵的形状一致：

1 2	`def squared_loss(y_hat, y): return (y_hat - y.reshape(y_hat.shape))**2 / 2`

然后需要定义一个优化算法，让参数沿着梯度反方向移动以进行优化。具体的理论知识参见[[线性回归]]。代码如下：

def sgd(params, lr, batch_size): # params为w和b，lr为学习率（步长），batch_size批量大小
	with torch.no_grad(): # 参数更新的过程不应该被记录进入计算图，无需计算梯度
		for param in params:
			param -= lr * param.grad / batch_size # param.grad在模型反向传播时生成
			param.grad.zero_() # 手动清空梯度值

定义训练过程。可以根据输出发现经过训练，预测值与真实值的差距（通过损失值体现）不断下降：

# 训练超参数定义
lr = 0.03 # 学习率
num_epochs = 3 # 数据集扫描次数
net = linreg # 确定训练使用模型
loss = squared_loss # 确定训练使用损失函数
# 训练过程
for epoch in range(num_epochs):
	for X, y in data_iter(batch_size, features, labels):
		l = loss(net(X, w, b), y) # 计算损失，构建计算图
		l.sum().backward() # 反向传播
		sgd([w, b], lr, batch_size) # 根据梯度更新参数值
	with torch.no_grad(): # 每扫描一次后评估训练进度
		train_l = loss(net(features, w, b), labels)
		print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
""" 输出：
epoch 1, loss 0.055857
epoch 2, loss 0.000265
epoch 3, loss 0.000052
"""

可以通过比较真实设置的参数和训练学到的参数来评估训练的成功程度，相关代码如下：

print(f'w的估计误差： {true_w - w.reshape(true_w.shape)}')
# w的估计误差： tensor([-0.0001, -0.0002], grad_fn=<SubBackward0>)
print(f'b的估计误差： {true_b - b}')
# b的估计误差： tensor([0.0007], grad_fn=<RsubBackward1>)

线性回归简洁实现

所谓简洁实现，就是使用深度学习框架来进行实现一个线性回归模型（利用了torch.utils中的data来进行一定的数据操作），首先进行包的引入和数据生成：

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

对于数据处理，现在可以使用一个PyTorch中的数据迭代器TensorDataset进行处理。只需要将输入的特征矩阵 $\textbf{X}$ 和标签 $b$ 构合并成一个矩阵（ $\begin{bmatrix} \textbf{X} | b \end{bmatrix}$ ）就可以转化为此数据迭代器对象。同时，此数据迭代器还可以使用DataLoader方法随机取出batch_size个数据点，以便后续训练：

def load_array(data_arrays, batch_size, is_train=True):
	dataset = data.TensorDataset(*data_arrays) # 构造PyTorch数据迭代器
	return data.DataLoader(dataset, batch_size, shuffle=is_train) 
	# shuffle决定取出的数据点是否是随机选取

batch_size = 10
data_iter = load_array((features, labels), batch_size)

print(next(iter(data_iter))) # 可以使用iter()将其转化为Python的Iterator

对于线性回归模型，可以直接使用PyTorch定义好的层（nn即神经网络的缩写），此处使用的是线性回归，因此只需要使用Linear并指定输入输出对象维度即可。此处将设定好的层放入了一个层容器Sequential中进行保存（以后访问这一层的模型只需要通过net[0]即可）：

1
2
3

from torch import nn

net = nn.Sequential(nn.Linear(2, 1))

使用nn.Linear()时需要定义初始化模型参数。定义的内容包括权重weight和偏差bias。初始化方法如下：

1 2	`net[0].weight.data.normal_(0, 0.01) # 权重均设为均值0方差0.01的随机数 net[0].bias.data.fill_(0) # 偏差直接设为0`

均方误差是常用的误差，可以直接使用MSELoss类计算（也称为平方 $L_2$ 范数）：

1	`loss = nn.MSELoss()`

同时使用sgd优化算法进行参数的优化也是常见的。此处只需要通过实例化SGD实例即可实现：

1	`trainer = torch.optim.SGD(net.parameters(), lr=0.03)`

训练过程代码和基础实现方式非常类似，代码如下：

num_epochs = 3
for epoch in range(num_epochs):
	for X, y in data_iter:
		l = loss(net(X), y) # 预测值y_hat用net(X)求出，再和真实y求损失
		trainer.zero_grad() # 将训练的参数梯度清零
		l.backward() # 利用内部方法直接反向传播
		trainer.step() # 将参数根据梯度进行优化
	l = loss(net(features), labels)
	print(f'epoch {epoch + 1}, loss {l:f}') # 每学习一轮进行损失展示
""" 输出：
epoch 1, loss 0.000227
epoch 2, loss 0.000098
epoch 3, loss 0.000098
"""

#深度学习 #课程笔记

学习Unity银河恶魔城游戏制作第二部分：瓦片、背景与摄像头上一篇

学习Unity银河恶魔城游戏制作第一部分：状态机设计与动作实现下一篇