学习D2L深度学习课程5:Softmax回归与Softmax回归实现

Softmax回归

Softmax

Softmax回归与线性回归针对的问题不同：线性回归解决的是回归问题、目标是针对输入估计一个连续值（例如根据房子的各个属性预测房价）；而Softmax回归解决的是分类问题、目标是针对输入对象预测一个离散类别（例如根据手写的数字图像分类其属于0~9哪个数字，这就是一个10类分类问题）。

回归与分类的差别如下：

回归：单连续数值输出，输出区间为自然区间 $R$ ，输出预测值和真实值的差别作为损失
分类：通常有多个输出，输出 $i$ 是将输入预测为第 $i$ 类的置信度

如果要解决分类问题，需要以下建模：

对类别进行一位有效编码（ $y_i$ 值代表其是否属于第 $i$ 类别）

\begin{split} & \textbf{y} = \begin{bmatrix}y_1, y_2, \dots, y_n \end{bmatrix} ^\top \\ & y_i = \begin{cases}1 \space , \space if \space i = y \\ 0 \space , \space otherwise\end{cases} \end{split}

使用均方损失训练
最大值作为模型预测： $\hat{y} = \arg\max_io_i$ （ $oi$ 代表输入对象属于 $i$ 类别的置信度）
最终的目标是需要更置信的识别正确类（正确类的置信度以一个阈值远高于其他类置信度），即： $o_y - o_i \geq \Delta(y, i)$
使用softmax使输出匹配概率。即输出值 $\hat{y_i}$ 代表输入属于此类别的概率。所有类对应输出的概率非负且和为一，通过 $o_i$ 求得：

\begin{split} & \hat{\textbf{y}} = softmax(\textbf{o}) \\ & \hat{y_i} = \frac {exp(o_i)}{\sum_{k}exp(o_k)} \end{split}

利用概率 $\textbf{y}$ 和 $\hat{\textbf{y}}$ 的区别作为损失

衡量真实概率和预测概率的区别需要使用交叉熵。交叉熵常用来衡量两个概率的区别，公式为：

H(\textbf{p}, \textbf{q}) = \sum_i -p_i\log(q_i)

如果使用交叉熵作为真实概率和预测概率间的损失函数，则公式推导如下。注意，由于真实概率向量 $\textbf{y}$ 是一个只有真实分类为1、其余分类概率均为0的向量，因此在交叉熵连加中只有真实分类（设为第 $y$ 类）对应非零，可以极大程度化简公式：

l(\textbf{y}, \hat{\textbf{y}}) = - \sum_i y_i \log \hat{y_i} = - \log \hat{y_y}

而对这个损失函数求 $o_i$ 的梯度，相当于对应类真实概率和预测概率的区别（偏导过程有点难，没推出来）：

\begin{split} \partial_{o_i}l(\textbf{y}, \hat{\textbf{y}}) = softmax(\textbf{o})_i - y_i = \frac {exp(o_i)}{\sum_{k}exp(o_k)} - y_i \end{split}

总结：

Softmax回归是一个多类分类模型
使用Softmax操作子得到每个类的预测置信度
使用交叉熵来衡量预测和标号的区别

损失函数

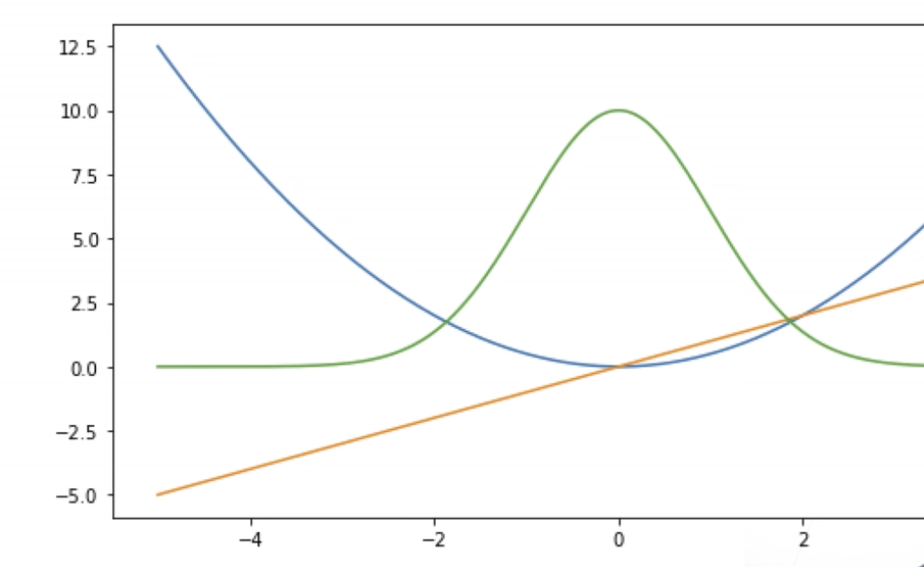
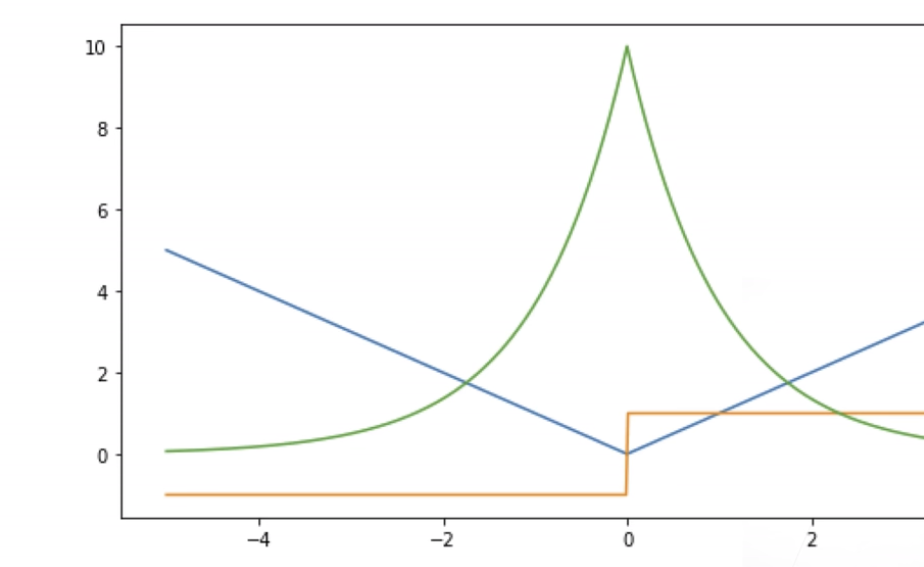
目前已经了解了几种常见的损失函数及图示（蓝色曲线表示真值为0时损失值随预测值的变化、绿线表示似然函数、黄线表示真值为0时梯度大小随预测值的变化）：

L2 Loss： $l(y, y') = \frac{1}{2}(y - y')^2$

可见，这种损失函数的梯度绝对值会随着预测值接近真实值而逐渐降低，也就是说当预测值和真实值相隔较远时，其更新幅度较大，而接近时更新幅度较小。这可能存在一个问题：算法设计者有时并不愿意当预测值偏差较大时损失函数也如此之大。因此可以采用L1 Loss解决这个问题：

L1 Loss： $l(y, y') = |y - y'|$

这种绝对值式的损失函数解决了上述远方梯度过大的问题，当真实值与预测值存在差异时，损失函数的梯度值绝对值永远为1。但是要注意使用绝对值作为损失函数时在零点（真实值等于预测值）不存在导数（梯度），同时在零点处存在一个梯度值由-1到1的剧烈变化。

Huber’s Robust Loss： $l(y, y') = \begin{cases}|y - y'|-\frac{1}{2} \space , \space if \space |y - y'| > 1 \\ \frac{1}{2}(y - y')^2 \space , \space otherwise \end{cases}$

这种损失函数结合了以上两种损失函数的优点，在预测值和真实值相隔较远时采用绝对值损失，使梯度绝对值不会过大；在预测值和真实值相隔较近时采用平方损失，使梯度绝对值在靠近零点时不会震荡或不存在，同时梯度绝对值也会下降。

Softmax回归实现

图像分类数据集

MNIST数据集在图像分类中广泛应用，但是作为基准数据集过于简单，后续训练中将会使用类似但是更加复杂的Fasion-MNIST数据集。相关库的引入如下：

import torch
import torchvision # pytorch关于计算机视觉的一些模型的实现库
from torch.utils import data # 小批量数据读取库
from torchvision import transforms # transform是torchvision中数据操作的相关库
from d2l import torch as d2l 

d2l.use_svg_display() # 以svg形式显示图片

接着需要通过框架中的内置函数下载Fashion-MNIST数据集并读取入内存。具体代码如下：

trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(
	root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
	root="../data", train=False, transform=trans, download=True)
	
print(len(mnist_train), len(mnist_test)) # 输出：60000 10000
print(mnist_train[0][0].shape) # 输出：torch.Size([1, 28, 28])

在读取时首先要使用transforms.ToTensor进行图像的预处理，此方法指示将图像转化为32位浮点数格式。然后分别下载Fashion-MNIST中的训练集和测试集，并需要规定下载内容的格式为之前指定图像预处理后的tensor格式，而非简单的图片。

下载完成后可以查看数据集的一些信息：该数据集中包含60000张训练集图像、10000张测试集图像；利用mnist_train[0][0]可以定位到第一张图像（第二维[0]代表图像，[1]代表label标号），发现图像大小为长宽28个像素、黑白（第一维阿尔法值长度为1）。

然后设置了一个返回数据集文本标签的可视化函数（针对输入labels中的各个数字标签，找到并输出对应的文字类别标签。例如从0找到t-shirt）：

def get_fashion_mnist_labels(labels):
	text_labels = [
		't-shirt', 'trouser', 'pullover', 'dress', 'coat', 'sandal',
		'shirt', 'sneaker', 'bag', 'ankle boot']
	return [text_labels[int(i)] for i in labels]

还设置了一个用以可视化数据集样本的函数：

def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):
	figsize = (num_cols * scale, num_rows * scale) # 计算画布尺寸
	_, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize) # 创建子图网格
	axes = axes.flatten()
	for i, (ax, img) in enumerate(zip(axes, imgs)): # 遍历显示每张图像
		if torch.is_tensor(img):
			ax.imshow(img.numpy())
		else:
			ax.imshow(img)
		ax.axes.get_xaxis().set_visible(False)
		ax.axes.get_yaxis().set_visible(False)
		if titles:
			ax.set_title(titles[i])
	return axes

这个函数的作用是批量化展示图像（将图像列表imgs按照num_rows行、num_cols列显示），同时可以添加每一张图的标签、通过scale控制图像的尺寸。

可以使用以上两个方法与之前自动求导实现中提到的DataLoader方法实现对于一个批次数据图像和标签的展示：

# X获取图像、y获取标签
X, y = next(iter(data.DataLoader(mnist_train, batch_size=18))) 
show_images(X.reshape(18, 28, 28), 2, 9, titles = get_fashion_mnist_labels(y))
d2l.plt.savefig("pic1.png") # 输出图片如下

现在就可以模拟训练时的数据读取真实情况。可以在DataLoader创建时指定要用多少个线程进行读取（即num_workers参数），一般会使用几个线程同时进行读取以保证读取速度快于训练速度，不会导致性能瓶颈。测试当前训练集一轮训练所需时间：

batch_size = 256
def get_dataloader_workers():
	return 4  

train_iter = data.DataLoader(
	mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers())

timer = d2l.Timer()
for X, y in train_iter:
	continue
print(f'{timer.stop():.2f} sec') # 输出：1.63 sec

最后就可以统合之前的所有内容，实现一个可以后续重用的Fasion-MNIST读取函数：

def load_data_fashion_mnist(batch_size, resize=None):
	trans = [transforms.ToTensor()] # 数据预处理
	if resize: # 后续如果需要更多像素的大图像，可以使用resize参数调整图像大小
		trans.insert(0, transforms.Resize(resize))
	# 将多个独立操作封装为原子化流水线，数据加载时自动按顺序执行
	trans = transforms.Compose(trans) 

# 下载数据集
	mnist_train = torchvision.datasets.FashionMNIST(
		root="../data", train=True, transform=trans, download=True)
	mnist_test = torchvision.datasets.FashionMNIST(
		root="../data", train=False, transform=trans, download=True)

# 使用DataLoader批量读取
	return (data.DataLoader(mnist_train, batch_size, shuffle=True,
							num_workers=get_dataloader_workers()),
			data.DataLoader(mnist_test, batch_size, shuffle=False,
							num_workers=get_dataloader_workers()))

Softmax基本实现

首先进行基本的库引入和数据的加载，设置批次读取量为256，并使用上一节中的Fashion-MNIST读取方法批量下载读取数据集：

import torch
from IPython import display
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

然后需要设置权重和偏移的初始值。注意：Softmax模型需求的输入是一个一维向量、输出的也是一个长度等于分类量的一维向量。而数据集中的图片为28个像素长宽的单通道图像，因此此处需要将图像像素信息拉伸拼接为一个28 * 28 = 784长度向量作为输入。

同时，我认为可以理解为这个输入的向量需要针对每一个分类输出都给出自己的权重，因此其实权重是一个输入元素数 * 输出分类数的矩阵、偏移也是一个长度为输出分类数的一维向量（我暂时理解为多个线性回归的拼接）。代码如下：

num_inputs = 784
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

根据Softmax回归中所讲，对于一个向量的Softmax操作如下：

\begin{split} & \hat{\textbf{y}} = softmax(\textbf{o}) \\ & \hat{y_i} = \frac {exp(o_i)}{\sum_{k}exp(o_k)} \end{split}

那么此时，对于一个矩阵来说，其Softmax等同于对每一行的行向量进行Softmax操作再整合（还是需要注意Softmax操作的目的：将参数转化为和为1的非负概率）：

softmax(\textbf{X})_{ij} = \frac {exp(\textbf{X}_{ij})}{\sum_{k}exp(\textbf{X}_{ik})}

在代码中定义一个矩阵的Softmax操作如下：

def softmax(X):
	X_exp = torch.exp(X)
	partition = X_exp.sum(1, keepdim=True) # 将矩阵每一行元素取值后相加，除法分母
	return X_exp / partition # 此处使用了广播机制，对齐了不同形矩阵

然后就可以定义求结果的网络方法了。注意：需要将输入内容转化为一个批次大小 * 照片转化一维向量长度的矩阵，才能进行计算，即和权重矩阵进行矩阵乘法后再和偏移分别相加：

1 2	`def net(X): return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)`

然后需要实现交叉熵损失函数。交叉熵损失函数的数学公式如下：

l(\textbf{y}, \hat{\textbf{y}}) = - \sum_i y_i \log \hat{y_i} = - \log \hat{y_y}

所以代码编写如下：

1 2	`def cross_entropy(y_hat, y): return -torch.log(y_hat[range(len(y_hat)), y])`

根据公式可知，每一组数据的所有预测值最终只需要真实值类别对应的预测值进行求对数再取反即可，因此对于每一组数据，只需要获得其真实值对应的类别预测值即可，这也正是y_hat[range(len(y_hat)), y]的意义：为每一组取出其真实类别的预测值。

然后进行正确率的计算，即统计当前批次中有多少组的预测正确（预测正确数除以每组数据量即为该组预测正确率）。代码如下：

def accuracy(y_hat, y):
	if len(y_hat.shape) > 1 and y_hat.shape[1] > 1: # 预测值为矩阵
		y_hat = y_hat.argmax(axis=1) # 找到每一行（代表一个数据）最大预测值类别作预测类别
	cmp = y_hat.type(y.dtype) == y # 比较预测类别和真实类别是否相等，输出布尔向量
	return float(cmp.type(y.dtype).sum()) # 转化为数字向量并求和，得知有多少组预测正确

然后可以再定义一个函数，用来对指定模型、指定组规模进行正确率的计算。代码如下：

def evaluate_accuracy(net, data_iter):
	if isinstance(net, torch.nn.Module): # 如果是torch.nn方式，直接切换评估模式
		net.eval()
	metric = Accumulator(2)
	for X, y in data_iter:
		metric.add(accuracy(net(X), y), y.numel())
	return metric[0] / metric[1]

其大致作用是：针对数据集的每一个批次，预测结束后（预测过程可自己设置并通过net参数传入）统计该组预测正确数据数，将预测正确数据数和该组总数据数输入累加器，最后就可以得到整个数据集的预测正确数和总数据数，然后相除就可以得到总正确率。

此处附加代码为累加器代码设置：

class Accumulator:
	def __init__(self, n):
		self.data = [0.0] * n
	def add(self, *args):
		self.data = [a + float(b) for a, b in zip(self.data, args)]
	def reset(self):
		self.data = [0.0] * len(self.data)
	def __getitem__(self, idx):
		return self.data[idx]

然后是单轮训练方法代码实现：

def train_epoch_ch3(net, train_iter, loss, updater):
	if isinstance(net, torch.nn.Module):
		net.train()
	metric = Accumulator(3)
	for X, y in train_iter:
		y_hat = net(X)
		l = loss(y_hat, y)
		if isinstance(updater, torch.optim.Optimizer): # 使用torchAPI的优化
			updater.zero_grad()
			l.backward()
			updater.step()
			metric.add(float(l) * len(y), accuracy(y_hat, y), y.size().numel())
		else: # 纯手工优化
			l.sum().backward()
			updater(X.shape[0]) # 根据批量大小放入updater
			metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
	return metric[0] / metric[2], metric[1] / metric[2] 
	# 第0元素损失和、第1元素正确个数、第2元素总个数

然后是整个训练过程的方法定义，整体思路就是定义整体轮数后在每一轮中调用单轮训练方法。代码如下：

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):
	for epoch in range(num_epochs):
		train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
		test_acc = evaluate_accuracy(net, test_iter)
		print(f'epoch:{epoch}, test_acc:{test_acc}')
	train_loss, train_acc = train_metrics
	print(f'finish! train_loss:{train_loss}, train_acc:{train_acc}')

对于模型中参数的优化方法，依然适用线性回归实现中定义的sgd方法。学习率与优化方法定义如下：

lr = 0.1

def updater(batch_size):
	return d2l.sgd([W, b], lr, batch_size)

最后就可以使用train_ch3函数进行整体训练了。训练代码及输出如下：

num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

""" 输出：
epoch:0, test_acc:0.7958
epoch:1, test_acc:0.8091
epoch:2, test_acc:0.8116
epoch:3, test_acc:0.8208
epoch:4, test_acc:0.8209
epoch:5, test_acc:0.8073
epoch:6, test_acc:0.8316
epoch:7, test_acc:0.8296
epoch:8, test_acc:0.8292
epoch:9, test_acc:0.8316
finish! train_loss:0.4470104190826416, train_acc:0.8483666666666667
"""

还可以对测试数据集的其中一组测试数据进行抽样预测。代码如下：

def predict_ch3(net, test_iter, n=6):
	for X, y in test_iter:
		break
	trues = d2l.get_fashion_mnist_labels(y)
	preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
	titles = [pred for true, pred in zip(trues, preds)]
	d2l.show_images(X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])
	d2l.plt.savefig("pic2.png")

predict_ch3(net, test_iter)

输出图像如下（标题为模型预测标签）：

Softmax回归简洁实现

开始的步骤同基本实现类似，需要引入一定库、设置每次读取数据的批量大小、读取Fashion-Minst数据集中的训练和测试集：

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

此时模型就可以通过nn进行构建，注意，由于Pytorch无法隐式的将一个多维的矩阵展平（正如前文所说Softmax需要一个一维向量输入），因此需要调用一个Flatten()层，此层可以讲输入第零维不变（代表不同数据点），其他维展平变成一个维度。同时还需要初始化权值：当检测到当前初始化的是Softmax的线性层时，就进行权值的均值0方差0.01的初始化。代码如下：

net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
	if type(m) == nn.Linear:
		nn.init.normal_(m.weight, std=0.01)

  net.apply(init_weights)

然后需要设置损失函数与优化算法。损失函数依然为交叉熵损失，可以直接使用nn.CrossEntropyLoss这一内置算法；优化算法使用torch.optim.SGD，对net网络中所有的参数进行学习率为0.1的优化：

1 2	`loss = nn.CrossEntropyLoss trainer = torch.optim.SGD(net.parameters(), lr=0.1)`

最后直接将这些设定好的内容输入上一节的train_ch3进行训练即可。代码如下：

num_epochs = 10
train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

""" 输出：
epoch:0, test_acc:0.7948
epoch:1, test_acc:0.8
epoch:2, test_acc:0.8202
epoch:3, test_acc:0.8166
epoch:4, test_acc:0.8265
epoch:5, test_acc:0.8313
epoch:6, test_acc:0.8317
epoch:7, test_acc:0.8276
epoch:8, test_acc:0.824
epoch:9, test_acc:0.8324
finish! train_loss:0.44748177267710365, train_acc:0.8476833333333333
"""

#深度学习 #课程笔记

学习D2L深度学习课程6:多层感知机和多层感知机实现上一篇

学习像素画课程2:线条和形状下一篇