学习D2L深度学习课程6:多层感知机和多层感知机实现

多层感知机

感知机

一个感知机的模型如下：给定一个向量输入x\textbf{x}，与其对应的向量权重w\textbf{w}和标量偏移bb，感知机做一个二分的标量输出（二分利用设置的σ(x)\sigma(x)函数实现）：

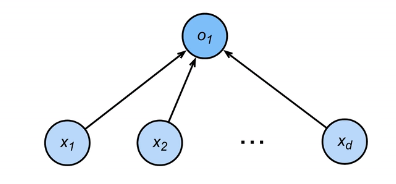
o=σ(<w,x>+b)     σ(x)={1 ,if x>0−1 , otherwiseo = \sigma(<\textbf{w}, \textbf{x}> + b) \space \space \space \space \space \sigma(x) = \begin{cases} 1 \space , if \space x > 0 \\ -1 \space , \space otherwise \end{cases}

实际上，感知机也是一个输出-1或1（或者0或1）的二分类问题。与前序问题对比：[[线性回归]]问题输出的是一个单一实数，而[[Softmax回归]]输出的是一组概率组成的向量（表示输入对象属于不同类的概率）。

一种传统的训练感知机参数的伪代码如下：

initialize w=0 and b=0repeat    if yi[<w,xi>+b]≤0 then        w←w+yixi and b←b+yi    end ifuntil all classified correctly\begin{split} &\textbf{initialize} \space \textbf{w} = 0 \space and \space b = 0\\ &\textbf{repeat} \\ &\space\space\space\space \textbf{if} \space y_i[<\textbf{w}, \textbf{x}_i> + b] \leq 0 \space \textbf{then} \\ &\space\space\space\space\space\space\space\space \textbf{w} \leftarrow \textbf{w} + y_i\textbf{x}_i \space and \space b \leftarrow b + y_i \\ &\space\space\space\space \textbf{end} \space \textbf{if} \\ & \textbf{until} \space all \space classified \space correctly \end{split}

这段代码的核心就是：一旦当前的预测值和数据的真实输出值不同（因为这里设置的二分输出是-1或1，只要预测值[<w,xi>+b][<\textbf{w}, \textbf{x}_i> + b]和真实值yiy_i不同号，即其乘积小于0，则代表预测失败），就需要更新权重和偏移参数。

也可以把这个过程等价于一个使用批量大小为1（相关概念见[[线性回归]]）进行的梯度下降，损失函数为下式：

ℓ(y,x,w)=max⁡(0,−y<w,x>)\ell (y, \textbf{x}, \textbf{w}) = \max(0, -y<\textbf{w},\textbf{x}>)

同时，一个感知机模型拥有一个普适的收敛定理。假设输入如下图所示：

对于数据也需要做两个假设：

  • 所有数据点均落在半径rr内
  • 存在一组参数（一个分类），能够将真实数据以一个余量ρ\rho划分为两类，即：

y(<x,w>+b)≥ρ  (∥w∥2+b2≤1)y(<\textbf{x}, \textbf{w}> + b) \geq \rho \space \space (\|\textbf{w}\|^2 + b^2 \leq 1)

如果输入真实数据能够满足以上两点，那么一个标准的感知机模型可以保证在r2+1ρ2\frac{r^2 + 1}{\rho^2}步后收敛（rr越大，数据范围越大，收敛越慢；ρ\rho越大，不同类数据间分离程度越大，收敛越快）。

但是感知机还是存在问题。例如感知机不能拟合XOR函数（如下图），核心就是因为其只能产生线性分割面，无法对这种输入进行有效分割：

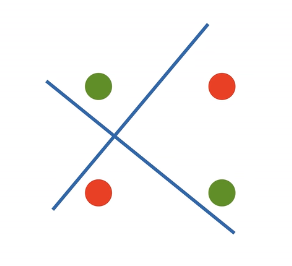
总结来说：感知机模型是一个二分类模型，其求解算法等价于使用批量大小为1的梯度下降，但其问题为无法拟合XOR函数。

多层感知机

想要解决XOR问题，一个简单的方法是多次分类，如下图：

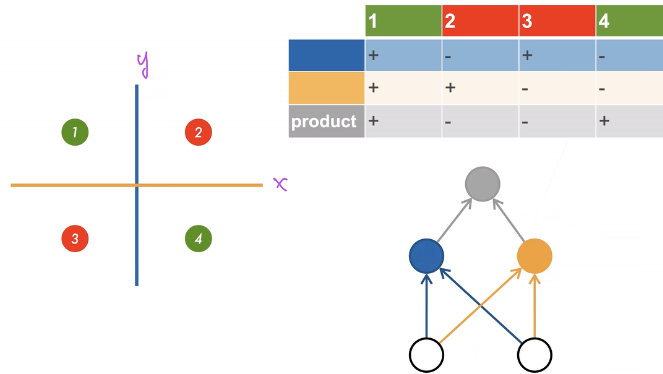
首先，分别使用单层感知机，实现蓝色和黄色线代表的分类，然后再根据不同的数据在两次分类中的结果，判定其最终分类。这正是多层感知机的原理。一个单隐藏层的多层感知机结构如下：

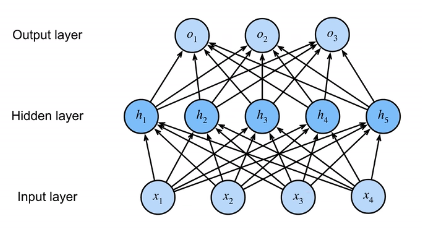
注意：隐藏层的大小是一个超参数。输入大小有数据决定，无法更改；输出大小由使用场景决定（例如要将输入分为多少类），同样无法改变，因此只有隐藏层的大小能够改变。

一个单隐藏层-单分类的模型相关参数如下：

  • 设输入大小（输入向量长度）为nn，隐藏层大小为mm
  • 输入为x∈Rn\textbf{x} \in R^n
  • 输入与隐藏层之间的感知机参数W1∈Rm×n\textbf{W}_1 \in R^{m \times n}，b1∈Rm\textbf{b}_1 \in R^m
  • 隐藏层与输出层之间的感知机参数w2∈Rn\textbf{w}_2 \in R^n，b2∈Rb_2 \in R

那么，相关值的计算如下（其中σ\sigma是按元素的激活函数）：

  • 隐藏层输出值向量：h=σ(W1x+b1)\textbf{h} = \sigma(\textbf{W}_1\textbf{x} + \textbf{b}_1)
  • 输出层单分类输出值：o=<w2,h>+b2o = <\textbf{w}_2, \textbf{h}> + b_2

要注意，σ\sigma这一激活函数需要为非线性的。因为一旦激活函数是一个线性函数，那么代入后会发现，最终这个模型还是等价于一个单层的线性感知机。举例：如果σ(x)=x\sigma(x) = x，即用本身作为一个线性激活函数，那么将隐藏层计算公式带入输出层计算公式，可以得到o=w2⊤W1x+b′o = \textbf{w}_2^{\top}\textbf{W}_1\textbf{x} + b^{'}，其实质还是一个线性函数。

一个比较传统的激活函数是Sigmoid激活函数，能够将输入量投影到(0,1)(0, 1)内。其公式为：

sigmoid(x)=11+e−xsigmoid(x) = \frac{1}{1 + e^{-x}}

其函数图像为：

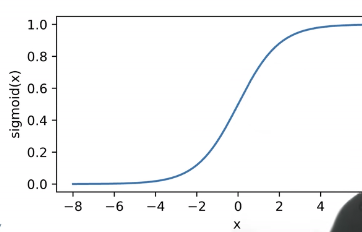
另一个激活函数是Tanh激活函数，能够将输入量投影到(−1,1)(-1, 1)内，其公式为：

tanh(x)=1−e−2x1+e−2xtanh(x) = \frac{1 - e^{-2x}}{1 + e^{-2x}}

其函数图像为：

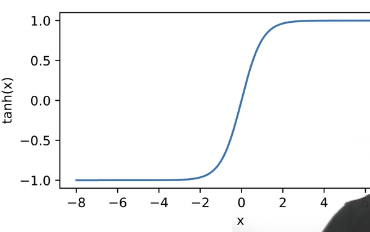
最后的常用激活函数是ReLU激活函数（rectified linear unit），其公式为（ReLU的优势在于简单，因为其他函数所用的指数项会造成很大的计算开销）：

ReLU(x)=max⁡(x,0)ReLU(x) = \max(x, 0)

其函数图像为：

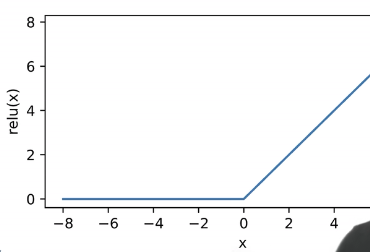
进行扩展：一个单隐藏层-多分类的模型相关参数如下：

  • 设输入大小（输入向量长度）为nn，隐藏层大小为mm，输出大小为kk
  • 输入为x∈Rn\textbf{x} \in R^n
  • 输入与隐藏层之间的感知机参数W1∈Rm×n\textbf{W}_1 \in R^{m \times n}，b1∈Rm\textbf{b}_1 \in R^m
  • 隐藏层与输出层之间的感知机参数W2∈Rk×m\textbf{W}_2 \in R^{k\times m}，b2∈Rk\textbf{b}_2 \in R^k

相关值的计算如下（其中σ\sigma是按元素的激活函数）：

  • 隐藏层输出值向量：h=σ(W1x+b1)\textbf{h} = \sigma(\textbf{W}_1\textbf{x} + \textbf{b}_1)
  • 输出层输出值向量：o=W2h+b2\textbf{o} = \textbf{W}_2\textbf{h} + \textbf{b}_2
  • 可以利用softmax(x)softmax(x)将输出向量进行概率归一化：y=softmax(o)\textbf{y} = softmax(\textbf{o})

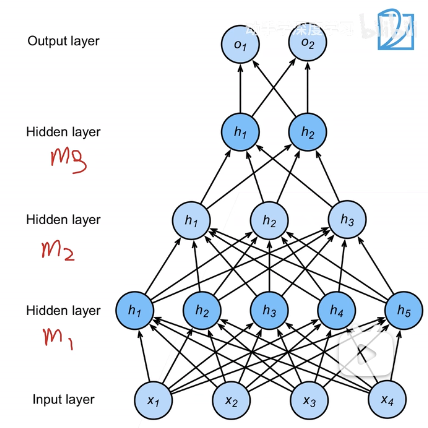
同样的，可以扩展变成多隐藏层-多分类模型。每一层都拥有自己的感知机权重参数Wi∈Rm×n, bi∈Rm\textbf{W}_i \in R^{m\times n}, \space \textbf{b}_i \in R^{m}。需要注意矩阵和向量的长度：mm代表当前层输出大小，nn代表当前层输入大小。然后就可以进行累加计算：

h1=σ(W1x+b1)h2=σ(W2h1+b2)h3=σ(W3h2+b3)o=W4h3+b4\begin{split} &\textbf{h}_1 = \sigma(\textbf{W}_1\textbf{x} + \textbf{b}_1)\\ &\textbf{h}_2 = \sigma(\textbf{W}_2\textbf{h}_1 + \textbf{b}_2)\\ &\textbf{h}_3 = \sigma(\textbf{W}_3\textbf{h}_2 + \textbf{b}_3)\\ &\textbf{o} = \textbf{W}_4\textbf{h}_3 + \textbf{b}_4 \end{split}

对于这样的多隐藏层多分类模型，其超参数包括：隐藏层数、每层隐藏层的大小。

总结来说：多层感知机使用隐藏层和激活函数来得到非线性模型，解决感知机线性模型无法处理XOR模型的问题；常用的激活函数为Sigmoid、Tanh、ReLU；当处理多输出（多类分类）问题时可以使用Softmax来进行处理；多层感知机的超参数包含隐藏层数和每层隐藏层大小。

多层感知机实现

多层感知机基础实现

首先，同样适用Fasion-MNIST数据集进行训练，因此需要对其训练集和测试集进行读取，并设置批量大小：

1
2
3
4
5
6
import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

目前，希望其实现一个具有单隐藏层的多层感知机，此隐藏层包含256个隐藏单元（输入图片共有784个像素，将其分为10类，此设置同[[Softmax回归实现]]）。根据输入、隐藏层、输出大小设置所需的两组权重矩阵和偏移向量参数。要注意，初始化权重矩阵需要使用随机、若设置为全0则隐藏层大小相当于被合并：

1
2
3
4
5
6
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True))
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True))
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

接着实现一个ReLU函数，对于隐藏层输出向量，将其每一个元素和0进行取大后的结果即为此激活函数的结果向量：

1
2
3
def relu(X):
	a = torch.zeros_like(X)
	return torch.max(X, a)

然后根据[[多层感知机]]中的公式进行模型的代码实现即可。注意，由于数据集中单个输入数据为一个28 * 28的图片，需要先把其拉直成为一个784长度的向量再进行输入：

1
2
3
4
5
6
def net(X):
	X = X.reshape((-1, num_inputs))
	H = relu(X @ W1 + b1)
	return (H @ W2 + b2)

loss = nn.CrossEntropyLoss() # 使用交叉熵损失作为损失函数

然后可以使用在[[Softmax回归实现]]中实现的训练函数进行训练：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

""" 输出：
epoch:0, test_acc:0.7363
epoch:1, test_acc:0.7481
epoch:2, test_acc:0.7455
epoch:3, test_acc:0.7624
epoch:4, test_acc:0.7677
epoch:5, test_acc:0.7721
epoch:6, test_acc:0.7638
epoch:7, test_acc:0.763
epoch:8, test_acc:0.7802
epoch:9, test_acc:0.7745
finish! train_loss:0.7446574956258138, train_acc:0.79895
"""

多层感知机简洁实现

首先，可以直接使用nn.Sequential进行模型构建，注意两点：由于输入图片为二维，需要使用一个nn.Flaten()层进行拉平；其次在隐藏层矩阵计算完毕后需要增加一个激活函数ReLU()层。还需要使用init_weights函数进行自定义神经网络权重的初始化。代码如下：

1
2
3
4
5
6
7
8
9
10
11
import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, 10))

def init_weights(m):
	if type(m) == nn.Linear:    
		nn.init.normal_(m.weight, std=0.01) # 仅针对线性层的权重参数，进行随机初始化

net.apply(init_weights) # 将初始化方法应用于网络的线性层中

然后只需要设置好参数进行运行即可，内容和基本实现一致：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=lr)

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

""" 输出：
epoch:0, test_acc:0.7146
epoch:1, test_acc:0.7543
epoch:2, test_acc:0.8113
epoch:3, test_acc:0.8274
epoch:4, test_acc:0.8189
epoch:5, test_acc:0.8238
epoch:6, test_acc:0.8265
epoch:7, test_acc:0.8147
epoch:8, test_acc:0.8444
epoch:9, test_acc:0.8454
finish! train_loss:0.38322266691525775, train_acc:0.8645833333333334
"""