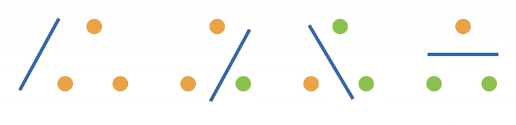学习D2L深度学习课程7:模型选择相关概念

数据集

在模型训练过程中存在两种误差：

  • 训练误差：模型在训练数据上的误差
  • 泛化误差：模型在新数据上的误差
    一个训练的最终目标是降低泛化误差，从结果上来说，模型的训练误差其实不被关心。

训练误差低并不代表后续的泛化误差也会低，就像以往的模拟考试成绩好并无法推出未来考试成绩一定好（例如模拟考试好的原因可能是拥有完备的预先准备）。

针对这些误差，也会存在不同的数据集：

  • 训练数据集：用来对模型进行训练
  • 验证数据集：一个用来评估模型好坏的数据集，可以从训练数据集中拿出部分数据组成（例如50%），要注意，验证数据集的结果是用来调整超参数的，因此不能和训练数据集混合（即不能用来训练）
  • 测试数据集：只用一次的数据集，是模型真正的应用场景，可以类比“未来的考试”，注意测试数据集不能和验证数据集混合（一般来说测试数据集应该是全新的，在训练过程中的不知道的数据），否则会影响超参数的调整

还存在一个问题：有可能出现数据不足的情况。此时可以使用K-折交叉验证方法进行计算。算法为：

  • 将训练数据分割为K块
  • 一共进行K轮训练，在第i轮训练中，选择第i块数据作为验证数据集，其余作为训练数据集
  • 将这K轮训练的验证数据集上的误差平均，作为最终的验证集误差
  • 常用K取值：5或10

总结来说：

  • 训练数据集：用来训练模型参数
  • 验证数据集：用来选择模型超参数
  • 数据集不够大：使用K-折交叉验证

过拟合和欠拟合

过拟合和欠拟合出现的大致条件如下：

模型容量（复杂度）\数据 简单 复杂
低 正常 欠拟合
高 过拟合 正常
也就是说，当面对简单数据时，如果选用过于复杂的模型，可能导致训练数据好是因为模型够复杂，能够记忆所有的训练数据标签，而非调参正确，这样在面对新的测试数据时有可能拟合效果不好；而面对复杂数据时，如果选用过于简单的模型，可能导致模型参数不足以有效拟合复杂数据，也导致面对测试数据拟合效果不好。

模型容量也可以被理解为拟合各种函数的能力。一个低容量模型难以拟合训练数据；而一个高容量的模型可以记住所有的训练数据。一个示意图如下：

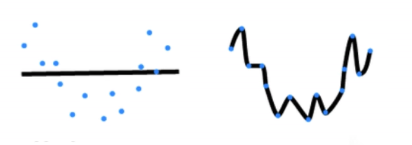
随着模型容量的提升（复杂度提升），其训练误差会不断下降至0，理论上无论训练数据集多大，都可以使用复杂的模型完全记忆。然而泛化误差并不会无限下降，当模型复杂度超过一个临界点之后，模型泛化误差就会开始不断回升（模型被无关噪音的细节干扰），而这个临界点就是模型的一个最优容量。模型容量对误差的影响示意如下：

由此，深度学习的核心就是：在保证模型容量足够大的前提下，使用各种手段限制模型容量，使得最终泛化误差的下降。

对于一个模型的容量，其估计相关准则如下：

  • 不同种类的算法之间，其模型容量难以被比较（例如树模型和神经网络之间的容量难以比较）
  • 当给定一种模型种类时，有两个影响容量的主要因素（例如下图两种感知机的容量比较）：
    • 参数的个数
    • 参数值的选择范围

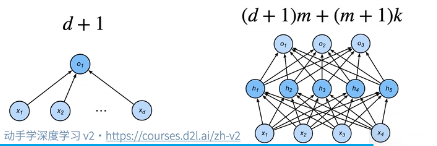
一个定量的概念是VC维。VC维是统计学习理论的一个核心思想：对于一个分类模型，VC等于一个最大的数据集大小：这个数据集无论如何给定标号，都存在一个模型能对其进行完美分类。

也就是说，可以把模型复杂度理解成：此模型能够完美分类的数据集的最大大小。

举一个例子：线性分类器的VC维：一个2维输入（x=[x1,x2]\textbf{x} = [x_1, x_2]）的感知机，其VC维为3。也就是说，任意三个输入，都可以用一个线性分类，将其完美的进行分类。但是，当存在四个输入时就有可能无法用线性分类器进行完美分类了（[[多层感知机]]中提到的XOR问题）。示意图如下：


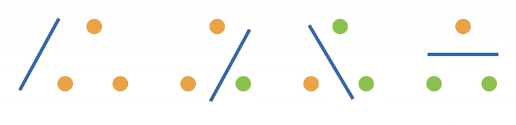
一些拓展：

  • 支持NN维输入的线性感知机的VC维是N+1N + 1
  • 一些多层感知机的VC维是O(Nlog⁡2N)O(N\log_2N)

VC维能够提供一个模型好的理论依据，因为它可以衡量训练和泛化误差之间的间隔。但是在深度学习中很少使用，因为衡量不准，且很难计算。

一个数据集的数据复杂度更加难以衡量，因为其拥有多个重要因素：

  • 样本个数
  • 每个样本的元素个数
  • 时间、空间结构
  • 多样性

总结来说：模型容量需要匹配数据复杂度，否则可能会导致欠拟合和过拟合；统计学提供了数学工具VC维来衡量模型复杂度，但是实际情况中一般靠观察训练误差和验证误差来进行感知。

代码例子

使用一个多项式拟合来探索这些概念。首先进行包的引入：

1
2
3
4
5
import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l

我们现在需要生成一些真实数据。生成的方法是：首先确定一个原型函数，然后在原型函数输出基础上，为其增加一个小的偏差值，最后就能形成一系列符合原型函数趋势，但又存在偏差的数据点。目前确定的原型函数为一个三阶多项式：

y=5+1.2x−3.4x22!+5.6x33!+ϵ where ϵ∼N(0,0.12)y = 5 + 1.2x - 3.4\frac{x^2}{2!} + 5.6\frac{x^3}{3!} + \epsilon \space where \space \epsilon \sim N(0, 0.1^2)

设置模型的参数数量最多为20（max_degree），训练集和验证集数据个数均为100，同时记录真实原型函数的各个参数：

1
2
3
4
max_degree = 20
n_train, n_test = 100, 100
true_w = np.zeros(max_degree)
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])

然后将xx进行随机初始化（所有xx使用features向量进行储存），然后利用这个公式计算对应的标签yy（所有yy使用labels向量进行储存）。相关代码如下：

1
2
3
4
5
6
7
8
features = np.random.normal(size=(n_train + n_test, 1)) #随机初始x
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1)) 
#x扩展为高维多项式特征
for i in range(max_degree):
	poly_features[:, i] /= math.gamma(i + 1) #每项对应除阶乘
labels = np.dot(poly_features, true_w) #每项对应乘系数参数
labels += np.random.normal(scale=0.1, size=labels.shape) #最终结果加随机偏移

可以对前两个数据点的相关信息进行输出检查：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
true_w, features, poly_features, labels = [
	torch.tensor(x, dtype=torch.float32)
	for x in [true_w, features, poly_features, labels]
]

print(features[:2])
print(poly_features[:2, :])
print(labels[:2])
""" 输出：
tensor([[ 0.0935],
        [-0.9050]])
tensor([[ 1.0000e+00,  9.3511e-02,  4.3722e-03,  1.3628e-04,  3.1860e-06,
          5.9585e-08,  9.2864e-10,  1.2406e-11,  1.4501e-13,  1.5066e-15,
          1.4089e-17,  1.1977e-19,  9.3331e-22,  6.7135e-24,  4.4842e-26,
          2.7955e-28,  1.6338e-30,  8.9870e-33,  4.6688e-35,  2.2978e-37],
        [ 1.0000e+00, -9.0495e-01,  4.0947e-01, -1.2352e-01,  2.7944e-02,
         -5.0577e-03,  7.6283e-04, -9.8618e-05,  1.1156e-05, -1.1217e-06,
          1.0151e-07, -8.3510e-09,  6.2977e-10, -4.3840e-11,  2.8338e-12,
         -1.7096e-13,  9.6696e-15, -5.1474e-16,  2.5879e-17, -1.2326e-18]])
tensor([5.1864, 1.7988])
"""

然后可以设置一个方法，求输入一个数据集后整体的损失均值：

1
2
3
4
5
6
7
8
def evaluate_loss(net, data_iter, loss):
	metric = d2l.Accumulator(2)
	for X, y in data_iter:
		out = net(X) #单数据点预测值
		y = y.reshape(out.shape) #单数据点真实值
		l = loss(out, y) #单数据点损失
		metric.add(l.sum(), l.numel())
	return metric[0] / metric[1] #总数据集损失均值

最后只需要定义训练函数即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
def train(train_features, test_features, train_labels, test_labels, num_epochs=400):
	loss = nn.MSELoss()
	input_shape = train_features.shape[-1]
	net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
	batch_size = min(10, train_labels.shape[0])
	train_iter = d2l.load_array((train_features, train_labels.reshape(-1, 1)), batch_size)
	test_iter = d2l.load_array((test_features, test_labels.reshape(-1, 1)), batch_size, is_train=False)
	trainer = torch.optim.SGD(net.parameters(), lr=0.01)

	for epoch in range(num_epochs):
		train_epoch_ch3(net, train_iter, loss, trainer)

	print('weight:', net[0].weight.data.numpy())

训练时，如果只提取使用多项式的前四个维度：train(poly_features[:n_train, :4], poly_features[n_train:, :4], labels[:n_train], labels[n_train:])，则其输出的训练参数是合理的：weight: [[ 5.010476 1.2354498 -3.4229028 5.503297 ]]，训练和验证集的损失情况也是合理的：

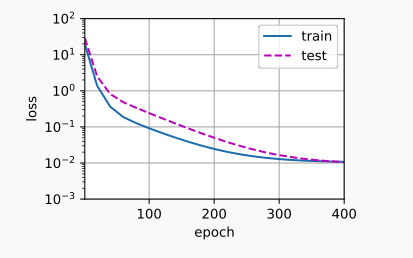
而如果线性函数进行拟合（也就是只使用多项式前四个维度，当作一个线性函数），那么训练和验证集的损失均难以下降：

反之，如果使用了过高阶的多项式函数进行拟合，则会出现过拟合现象，虽然训练损失可以有效降低，但是在测试集上进行实验时，测试损失依然较高：